Géométrie analytique

[poincaré]

Salutations amis matheux.

Je rencontre des difficultées dans le domaine de la géométrie analytique ^^.

On place E, F et G tels que AE = 1/4 AB, AF = 1/2 AC et AG = 3/4 AD.

On travaille dans le repere (A;AB;AC;AD)

1) Quelles sont les coordonnées du point Q commun a la droite D, intersection des plans (BCD) et (EFG), et au plan (ABC).

2) Quelles sont les coordonées du point R commun a la droite D et au plan (ABD) ?

j'ai commencé a répondre a la premiere mais je bloque un peu ^^

Si un point appartient au plan (EFG) ses coordonnées x,y et z s'obtiennent par la relation :

(les points seraient coplanaires, et définis par la relation (le point M est a titre d'exemple) EM = a EF + b EG)

x = 1/4 a -1/4 b + xe
y = 1/2 a + ye
z = 3/4 b + ze


Si un point appartient au plan (BCD) ses coordonnées x,y et z s'obtiennent par la relation :

(les points seraient coplanaires, et définis par la relation (le point M est a titre d'exemple) BM = a BC + b BD)

x = -1 a -1 b + xb
y = 1 a + yb
z = 1 b + zb

Et enfin Si un point appartient au plan (ABC) ses coordonnées x,y et z s'obtiennent par la relation :

(les points seraient coplanaires, et définis par la relation (le point M est a titre d'exemple) AM = a AB + b AC)

x = 1 a + xa
y = 1 b + ya
z = za

la question est 1)Quelles sont les coordonnées du point Q commun a la droite D, intersection des plans (BCD) et (EFG), et au plan (ABC).
comment s'y prend-on ? ^^ Idem pour la deux je vous prie.

Merci d'avance ! :)

Poincaré.

[poincaré]

Y a t-il des personnes présentes ? ^o^

[Zebulon]

Bonjour,
il manque au moins les coordonnées de A, B et C pour la première question.
On a .

[poincaré]

On travaille dans le repere (A;AB;AC;AD)

donc A(0;0;0) B(1;0;0) C(0;1;0) et D(0;0;1)

:we:

[Zebulon]

Oui, c'est vrai. Alors vous pouvez trouver une équation des droites (BC) et (EF) et en déduire leur point d'intersection.

[poincaré]

Exact. Cependant j'ai oublier comment procéder.

Il me semble qu'il faille résoudre une équation des droites en question et en dédure les coordonnées des points en question ?

Marci d'avance.

[Imod]

Pour continuer l'idée de Zebulon : {Q}=(BC)inter(EF) or dans le plan (ABC) en regardant les coefficient directeurs et ordonnées à l'origine des droites :
(BC):y=-x+1 et (EF):y=-2x+1/2 .
On calcule xQ et yQ comme point d'intersection des deux droites et comme Q est dans (ABC) , zQ=0 .

Imod

[Zebulon]

Pour déterminer un système d'équations de la droite (BC) :
on commence par déterminer les coordonnées de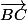 , qui sont .
Soit M(x,y,z) un point de l'espace,
alors si et seulement s'il existe 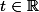tel que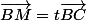
ssi il existe t tel que
ssi .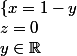
On fait de même avec la droite (EF), et on résout le système formé de toutes les équations des droites (BC) et (EF).