Frontière et adhérence

[mehdi-128]

Bonsoir,

Je reprends les maths depuis quelques mois après 7 ans d'arrêt et aucun souci particulier de compréhension sur le calcul intégral, les suites de fonctions et les séries (les séries entières c'est un peu dur quand même), mais en topologie je nage complètement. J'avais déjà pas compris grand chose en prépa.

J'arrive pas à visualiser ce qu'est l'adhérence et l'intérieur même après avoir lu 50 définitions. Je comprends pas pourquoi l'adhérence d'une partie contient la partie.

Y a pas des dessins pour pouvoir comprendre ces notions ?

[chan79]

Je comprends pas pourquoi l'adhérence d'une partie contient la partie.

Salut
L'adhérence d'une partie d'un espace topologique est le plus petit ensemble fermé contenant cette partie.
Dans , l'adhérence de ]1;2[ est [1;2]

[Pseuda]

Bonjour,

Ou aussi : l'adhérence d'une partie est l'ensemble des limites de suites convergentes d'éléments de cette partie (propriété de l'adhérence).

Donc si on prend un élément x de cette partie, il est limite d'une suite constante donc convergente d'éléments de la partie tous égaux à x, donc il appartient à l'adhérence de la partie.

Autrement dit, toute partie est incluse dans son adhérence.

[Pseuda]

Je me représente l'adhérence d'une partie A avec un dessin : je dessine A comme une grosse patate sur la feuille de papier.

L'adhérence de A est A avec le trait qui le délimite.
L'intérieur de A est A sans le trait qui le délimite.

A lui-même peut avoir des points sur le trait, ou non.

[aviateur]

Bonjour
Si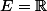 , comment je dessine une grosse patate? (boutade).

En effet @pseuda à raison.

Mais @medhi-182 tu peux aussi essayer de regarder
le sous-ensemble de R (que je note H ) et qui est constitué des nombres

quelle est son intérieur, son adhérence...?

Même question avec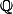 comme sous-ensemble de R.

[Ben314]

Salut,
A mon avis, si tu veut qu'on t'aide, le premier truc que tu devrait préciser c'est le contexte dans lequel tu envisage d'étudier le topologie (Topologie générale / Espaces métriques / Espaces vectoriels normés) vu qu'il y a quand même de petites différences (par exemple la caractérisation donné par Pseuda de l'adhérence n'est pas valable dans le contexte de la topologie générale)

Sinon, effectivement, au niveau "visuel", le truc le plus simple c'est la notion de frontière d'un ensemble (le "trait qui la délimite" comme dit Pseusda) qu'on peut parfaitement définir :
Par exemple, dans le cadre des espace métrique, on peut définir la frontière d'une partie A d'un espace métrique X, comme étant l'ensemble des x de X tel que toute boule centré en x, aussi petite soit elle, continent à la fois des points de A et des points qui ne sont pas dans A.
Ensuite, une fois la notion de frontière clairement définie, on a les caractérisation (qui me semblent très visuelles) suivantes :
- Une partie A de X est fermée lorsque la frontière de A est contenue dans A.
- Une partie A de X est ouverte lorsque la frontière de A n'a aucun point commun avec A.
(donc si une partie A contient une partie de sa frontière, mais pas toute sa frontière, alors cette partie n'est ni ouverte, ni fermée. Et dans l'autre sens, si la frontière de A est vide, alors A est à la fois ouverte et fermée)

Par contre, bien que ce soit sans doute la chose la plus "visuelle", la notion de frontière d'une partie A n'est pas super utile pour faire de la topologie donc il y a peu d'auteurs qui font le choix de commencer par définir la notion de frontière pour ensuite définir la notion de partie ouverte et de partie fermée à l'aide des caractérisation çi dessus.

[mehdi-128]

J'étudie seulement la topologie des espaces normés car je révise pour le CAPES. Je révise le programme de Sup et Spé. Les espaces métriques et la topologie générale ne sont pas au programme.

[mehdi-128]

Je me représente l'adhérence d'une partie A avec un dessin : je dessine A comme une grosse patate sur la feuille de papier.

L'adhérence de A est A avec le trait qui le délimite.
L'intérieur de A est A sans le trait qui le délimite.

A lui-même peut avoir des points sur le trait, ou non.

Ah je vois, l'adhérence il faut qu'on puisse trouver une boule de n'importe qu'elle rayon telle que l'intersection de cette boule avec la patate ne soit pas réduit àl'ensemble vide donc forcément le point a qui est adhérent est soit dans la patate soit à la frontière c'est ça ?

Pour l'intérieur, on doit pouvoir toujours inclure une boule de n'importe quel rayon qui soit incluse dans la patate donc c'est tout les points à l'intérieur de la patate mais pas la frontière.

[mehdi-128]

Bonjour
Si , comment je dessine une grosse patate? (boutade).

En effet @pseuda à raison.

Mais @medhi-182 tu peux aussi essayer de regarder
le sous-ensemble de R (que je note H ) et qui est constitué des nombres

quelle est son intérieur, son adhérence...?

Même question avec comme sous-ensemble de R.

J'ai :

J'y arrive pas à trouver l'intérieur et l'adhérence de H et de Q.

je vois pas le lien avec les définitions données avec les patates.

[Pseuda]

Je ne parle aussi que des espaces vectoriels normés, que je connais. J'essaie aussi de me remettre en tête la sup et la spé.

Oui la patate est très simplificatrice, elle peut comporter par exemple des trous et des points isolés, ce qui agrandit la frontière. Les points isolés n'ont pas d'intérieur, donc ils ne sont pas à l'intérieur de A. Mais ils sont dans l'adhérence.

@medhi c'est ça, je vois l'adhérence de A comme une partie qui colle à A, pour laquelle il n'y a pas d'espace vide entre un point de l'adhérence et A. Je vois un point de l'intérieur de A comme au contraire un point entièrement ceinturé par une partie de A (un voisinage ou une boule).

@aviateur Concernant l'adhérence de Q, ne faut-il pas préciser dans quel evn on se place. Dans R, c'est R. Dans C, c'est C.

A ce propos, il y a une question que je me pose depuis longtemps : ne pourrait-on pas considérer Q comme un evn sur Q muni de la norme valeur absolue. Dans ce cas, quelle serait l'adhérence de Q dans l'evn Q ? (car il y a des suites de Q qui ne convergent que dans R)

[mehdi-128]

Pour montrer que Q est dense dense dans R c'est à dire que Q barre égal à R faut montrer que toute suite de rationnels à une limite réelle.
Mais je sais pas c'est quoi une suite de rationnels.

[Pseuda]

Pour l'adhérence de A={1/n, n e N*}, c'est A augmenté de 0, car toute boule de centre 0 contient au moins un élément de A. Oui la vision de la patate est décidément très simplificatrice. Tout autre élément n'est pas dans l'adhérence, par exemple 2/3 n'y est pas car ]2/3-1/10 , 2/3+1/10[ ne contient pas d'élément de A.

[Pseuda]

Pour montrer que Q est dense dense dans R c'est à dire que Q barre égal à R faut montrer que toute suite de rationnels à une limite réelle.
Mais je sais pas c'est quoi une suite de rationnels.

Ce n'est pas tout à fait ça. Toute suite convergente de rationnels a une limite réelle, pas forcément rationnelle ni forcément irrationnelle (suite constante égale à 1/3).

Non, il faut montrer que tout réel peut s'écrire comme limite d'une suite de rationnels (R inclus dans Q barre). Par exemple la suite U(n+1)=1/2 (Un+ 2/Un) avec U_0=1, est une suite de rationnels qui converge vers V2.

[mehdi-128]

C'est quoi votre définition de la boule ici ?
Je comprends pas pourquoi 0 appartient à l'adhérence de A.

[Pseuda]

Pour tout r>0, B(0,r) inter A est non vide. Elle contient 1/n avec n>E(1/r).

Pour moi, B(0,r)=]-r,+r[. On est dans R.

[mehdi-128]

Pseuda je crois avoir compris pour A :

On prend l'intervalle : donc 0 est adhérent à A.

Donc :

[Pseuda]

Il faut montrer que TOUTE boule de centre 0 contient un élément de A. Pas seulement une boule. (sinon j'élargis le rayon autant que je veux et elle va bien finir par contenir un élément de A).

(J'écris avec des majuscules car je suis sur téléphone).

[mehdi-128]

En effet Pseuda vous avez raison y des subtilités dans la définition.

Pour l'adhérence on a donc : 0,1,1/2,....,1/n

Je m'intéresse à l'intérieur maintenant : a est dans l'intérieur de H

Il faut montrer :

Donc l'intérieur de H c'est H privé de 1 et de 1/n ?

En effet on peut trouver aucun intervalle de la forme :

[mehdi-128]

Je comprends pas les cours du supérieur et de prépa, on nous parle de choses ultra théoriques et compliquées et on n'explique jamais sur des exemples simples et concrets au final on comprend jamais rien.

J'aurais aimé avoir des profs qui partent des exemples basiques au lieu de nous perdre dans leur théories et démonstration alors qu'on a même pas compris la base de la base.

[aviateur]

Bonjour
Il y a tellement de posts que je risque de dire des choses un peu à côté.
Néanmoins si @medhi se contente de la topologie dans un espace E muni d'une norme (disons N ) je tiens à faire remarquer qu'il y a une métrique naturellement associée qui est : d(x,y)=N(x-y) pour tout x et y dans E.
Ensuite il devrait revenir aux définitions et notions de boules, voisinages, d'ouverts et de fermés.
Et puis d'essayer et de commencer à comprendre tout cela avec des espaces "simples" (i.e dimension finie où la topologie ne dépend pas la norme.)
Par exemple R muni de la distance usuelle et R^2 muni de la norme usuelle (i.e euclidienne).

Pour R^2 bien entendu on peut prendre (et il faut) prendre des exemples qui ressemble à des patates mais
bien entendu une partie de R^2 n'a pas toujours l'allure d'une patate.

Maintenant c'est clair que quand je parle de Q c'est en tant que sous ensemble de R et sa fermeture est bien R.

Mais si on regarde Q comme sous ensemble de C sa fermeture est encore R (et non pas C @pseuda?).