Bonjour,
Je souhaiterai comprendre la différence entre ces deux formules afin de vérifier la somme d'une suite arithmétique :
1) n(n+1)/2
2) nombre de termes x (1er terme + dernier terme/2)
Merci beaucoup.
Somme des termes consécutifs d'une suite arithmétique
3 messages
- Page 1 sur 1
Re: Somme des termes consécutifs d'une suite arithmétique
TchouTchou a écrit:Bonjour,
Je souhaiterai comprendre la différence entre ces deux formules afin de vérifier la somme d'une suite arithmétique :
1) n(n+1)/2
2) nombre de termes x (1er terme + dernier terme/2)
Merci beaucoup.
La première formule correspond à la somme des n premiers entiers consécutifs.
1+2+....+n = n(n+1)/2
Cette formule s'obtient en utilisant un rectangle de longueur n de largeur (n+1). Bien entendu la suite (1,2,...n) est arithmétique de raison 1 de premier terme 1 et de dernier terme n.
La seconde formule il n'est pas indispensable de l'apprendre par coeur si on ne maitrise pas la première (enfin les formules qui lui ressemblent). Je te donne un exemple, suppose que tu as une autre suite arithmétique et que tu veux calculer:
3 + 5 + 7+ 9+11+13+ 15 (on veut jusqu'à 15)
Tu peux la décortiquer: 3 + (3 + 2) + (3+2+2)+...(3+2×6)
3 apparait autant de fois qu'il y a des termes donc 6 fois.
Puis tu as les 2 (la raison), qui figurent comme suit 2+2×2+...+2×6=2(1+2+...+6)
Tu peux maintenant utiliser la formule d'avant pour calculer (1+...+6) avec n(n+1)/2
Au final la somme S se calcule sans problème.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Somme des termes consécutifs d'une suite arithmétique
salut


sachant que pour tous entiers m et n :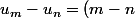r) où r est la raison de la suite arithmétique ...
où r est la raison de la suite arithmétique ...
sachant que pour tous entiers m et n :
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
