Somme de termes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
nukejacass
- Membre Naturel
- Messages: 18
- Enregistré le: 03 Sep 2016, 17:47
-
 par nukejacass » 18 Sep 2016, 18:19
par nukejacass » 18 Sep 2016, 18:19
Bonjour,
Je ne comprends pas pourquoi dans cette égalité on prend (n-m+1) terme et non pas (n-m)

= α+α+...+α=(n−m+1)α
Ensuite, je ne discerne pas bien la différence entre ces deux sommes :
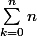
= n(n+1)
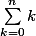
=
}{2})
Merci d'avance
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 18 Sep 2016, 18:32
par jlb » 18 Sep 2016, 18:32
Combien il y a de termes de 3 à 6 par exemple :3,4,5,6 et 6 -3 =3 et pas 4!!
La première contient n+1 termes ( de 0 à n) égaux à n cela donne (n+1) fois la valeur n soit (n+1)n
La dernière contient n termes (de 1 à n) égaux à n
-
nukejacass
- Membre Naturel
- Messages: 18
- Enregistré le: 03 Sep 2016, 17:47
-
 par nukejacass » 18 Sep 2016, 18:37
par nukejacass » 18 Sep 2016, 18:37
Merci pour votre réponse,
Mais du coup ça serait plutôt n-m termes si je suis votre raisonnement et non pas (n-m+1)
Pour la 2e je me suis trompé, j'ai corrigé, mais je ne comprends toujours pas
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 18 Sep 2016, 18:45
par jlb » 18 Sep 2016, 18:45
reprends à t^te reposée l'exemple de 3 à 6: tu as 3,4,5 et 6 soit 4 nombres!! et 6-3 ne fait que 3 donc on ajoute 1.
C'est le principe des piquets et des écarts entre les piquets: la différence donne le nombre d'écarts et tu rajoutes 1 pour le nb de piquets!!
| | | | | tu as ici 4 écarts et pour cela il faut 5 piquets
Modifié en dernier par
jlb le 18 Sep 2016, 19:24, modifié 1 fois.
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 18 Sep 2016, 18:51
par jlb » 18 Sep 2016, 18:51
Pour le deuxième le k prend les valeurs de 0 à n, cela signifie qu'il faut calculer 0+1+2+3+...+ n
2 versions: c'est la somme des n+1 premiers termes d'une suite arithmétique de raison 1 et 1er terme 0 soit (n+1)(u0 + Un+1)/2 = (n+1)(0+n)/2 =(n+1)n/2
version2: tu comptes 2 fois la somme: 1 + 2 + ..... + n + 1+2 +....+ n =(1+n) + (2 + n-1) + (3 +n-3) .... = n(n+1)
(tu regroupes le premier avec le dernier ça fait n+1, le deuxième avec l'avant dernir ça fait n+1 et ainsi de suite)
et tu conclus en divisant par 2 car tu as compté 2 fois la somme.
-
nukejacass
- Membre Naturel
- Messages: 18
- Enregistré le: 03 Sep 2016, 17:47
-
 par nukejacass » 18 Sep 2016, 18:55
par nukejacass » 18 Sep 2016, 18:55
AH oui j'ai compris pour les deux merci beaucoup jlb
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités