Bonjour tout le monde!
Voilà je cherche à calculer une somme à "bornes variables", allant de 5 en 5, et en ne gardant que les termes positifs de la somme suivante :
;)T=;)i,j P*R*(1-i*j)
Avec i=]100-2x ; 100+2x] x,y étant des réels >0
j=]100-2y ; 100+y] i et j doivent être des multiples de 5 (on arrondi au multiple de 5)
Ce sera peut-être plus clair sous forme de matrice :
......i: 0 5 10 [...] 150
j:
0 T(0,0) [...] T(0,150)
5 ................................
10 ................................
[...] ................................
200 T(200,0).........T(200,150)
Matrice sur laquelle on ne somme que les valeurs de T positives et les valeurs de T pour lesquelles i et j sont dans leur intervalle respectif
Ex : si x=10 et y=11, alors i=[85;120] (85 et non 80 car intervalle semi ouvert) et j=[80,110] le tout modulo 5
Voici ce que j'ai fais :
;)(T>0)=;)i,j P*R*(1-i*j)
;)(T>0)=P*R*(;)[i,j] 1 - ;)i*;)j)
Or ;)[i,j] 1 =nb termes en i * nb de termes en j
nb de termes en i=E[((100+2x)-(100-2x)+1)/5]=E[(4x+1)/5] avec E(x):fonction valeur entière
nb de termes en j=E[(3y+1)/5]
Donc ;)(T>0)=P*R*(E[(4x+1)/5]*E[(3y+1)/5] - ;)i*;)j)
Or ;)i=nb de termes* (dernier+1er)/2 (suite arithmétique)
;)i=E[(4x+1)/5]*(100+2x+100-2x)/2=E[(4x+1)/5]*100
De même ;)j=E[(3y+1)/5]*(100-(1/2)y)
;)(T>0)=P*R*E[(4x+1)/5]*E[(3y+1)/5]*[1-100*(100-(1/2)y)]
;)(T>0)=P*R*E[(4x+1)/5]*E[(3y+1)/5]*[50y-9999]
Problème : - l'utilisation de la fonction valeur entière me paraît un peu trop complexe à manier ensuite, n'y aurait-il pas autre chose à faire?
- ici j'ai aussi compter les termes négatifs alors que je ne voulais que les positifs, comment faire? Passer par les complexes ? :mur:
J'espère ne pas vous avoir endormis
Merci de votre aide :lol3:
Somme des termes uniquement positifs avec bornes variables
13 messages
- Page 1 sur 1
Je reformule
Je me rends bien compte que mon premier message n'était pas compréhensible donc je reformule avec du Latex :
Je cherche bien un calcul explicite, un résultat qui serait fonction de x et y
Je cherche à calculer la somme suivante :
\right $$)
P et R constantes, x et y des réels positifs
Mais deux conditions sont imposées :
- ne doit être sommé que les termes positifs, ce qui équivaut donc aux combinaisons $i\times j$ pour lesquelles $i\times j$<10 000 mais je ne sais pas comment inclure cette conditions dans le calcul
- i et j doivent être des multiples de 5 donc on les arrondis aux multiples de 5 le plus proche
ex:si x=11, alors l'intervalle de i devient : i=[80;120]
Merci d'avance
Je cherche bien un calcul explicite, un résultat qui serait fonction de x et y
Je cherche à calculer la somme suivante :
P et R constantes, x et y des réels positifs
Mais deux conditions sont imposées :
- ne doit être sommé que les termes positifs, ce qui équivaut donc aux combinaisons $i\times j$ pour lesquelles $i\times j$<10 000 mais je ne sais pas comment inclure cette conditions dans le calcul
- i et j doivent être des multiples de 5 donc on les arrondis aux multiples de 5 le plus proche
ex:si x=11, alors l'intervalle de i devient : i=[80;120]
Merci d'avance
Bonsoir
C'est plutôt d'un algorithme et d'un programme informatique dont tu as besoin.
Pour le problème des multiples de 5, on trouve les bornes de sommation en tant que multiple de 5 qu'on ramène à leurs quotients par 5 ([80;120] devient [16;24]. Faire la même chose pour l'autre indice.
Précision:
1) C'est les bornes seulement de sommation qui doivent être des multiples de 5 avec des pas de 1 ou c'est les bornes et les indices qui sont des multiples de 5, c'est ce que je vais traiter.
2) x et y sont des réels positifs, les indices i et j peuvent-ils prendre des valeurs négatives, la valeur 0, si i et j sont de signes opposés, la condition est alors automatiquement vérifiée.
est alors automatiquement vérifiée.
La somme\right $$)
s'écrit
\right) = \sum_{i=i_0}^{i_1} \left (\sum_{j=j_0}^{j_1} PR \left (1-\frac{i}{20} \times\frac{j}{20})\right\right) $$)
Le problème du pas de 5 dans la sommation que tu as donnée est ramené à un pas de 1 dans les sommations que j'ai données . La condition que
que
tu t'es imposée devient alors: dans
dans \right)
En ajoutant cette condition, on peut alors écrire:
 \right)= \sum_{i_0 \le i \le i_1} \left( \sum_{j_0 \le j \le j_1,ij<400} \text{ }PR \left( 1-\frac{ij}{400} \right) \right))
Remarque: Si i=0 ou j=0, le terme à ajouter) devient
devient 
Laos a écrit:Je me rends bien compte que mon premier message n'était pas compréhensible donc je reformule avec du Latex :
Je cherche bien un calcul explicite, un résultat qui serait fonction de x et y
Je cherche à calculer la somme suivante :\right $$)
P et R constantes, x et y des réels positifs
Mais deux conditions sont imposées :
- ne doit être sommé que les termes positifs, ce qui équivaut donc aux combinaisons $i\times j$ pour lesquelles $i\times j$<10 000 mais je ne sais pas comment inclure cette conditions dans le calcul
- i et j doivent être des multiples de 5 donc on les arrondis aux multiples de 5 le plus proche
ex:si x=11, alors l'intervalle de i devient : i=[80;120]
Merci d'avance
C'est plutôt d'un algorithme et d'un programme informatique dont tu as besoin.
Pour le problème des multiples de 5, on trouve les bornes de sommation en tant que multiple de 5 qu'on ramène à leurs quotients par 5 ([80;120] devient [16;24]. Faire la même chose pour l'autre indice.
Précision:
1) C'est les bornes seulement de sommation qui doivent être des multiples de 5 avec des pas de 1 ou c'est les bornes et les indices qui sont des multiples de 5, c'est ce que je vais traiter.
2) x et y sont des réels positifs, les indices i et j peuvent-ils prendre des valeurs négatives, la valeur 0, si i et j sont de signes opposés, la condition
La somme
s'écrit
Le problème du pas de 5 dans la sommation que tu as donnée est ramené à un pas de 1 dans les sommations que j'ai données . La condition
tu t'es imposée devient alors:
En ajoutant cette condition, on peut alors écrire:
Remarque: Si i=0 ou j=0, le terme à ajouter
Bonjour,
Merci pour ta réponse!
Ce sont bien à la fois bornes et indices qui sont multiples de 5, par contre i et j ne peuvent prendre des valeurs négatives ni nulles.
J'ai appliqué ce que tu m'as conseillé et ça m'a bien avancée!
Mais je ne vois pas comment m'en sortir dans la manipulation des bornes de j :
car équivaut à
équivaut à  ce qui constitue donc notre nouvelle borne supérieure
ce qui constitue donc notre nouvelle borne supérieure
La somme devient donc \right))
De ce fait si on veut calculer ou encore
ou encore ) après avoir éclater la somme, on se retrouve avec
après avoir éclater la somme, on se retrouve avec  qui n'est pas "calculable"...
qui n'est pas "calculable"...
Je l'ai donc remplacé par son équivalent en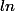 soit
soit -ln(j_0)) puis-je faire ça et est-ce judicieux ? :hein:
puis-je faire ça et est-ce judicieux ? :hein:
Merci
Merci pour ta réponse!
Ce sont bien à la fois bornes et indices qui sont multiples de 5, par contre i et j ne peuvent prendre des valeurs négatives ni nulles.
J'ai appliqué ce que tu m'as conseillé et ça m'a bien avancée!
Mais je ne vois pas comment m'en sortir dans la manipulation des bornes de j :
car
La somme devient donc
De ce fait si on veut calculer
Je l'ai donc remplacé par son équivalent en
Merci
programme informatique
Deltab a écrit:C'est plutôt d'un algorithme et d'un programme informatique dont tu as besoin.
Un programme informatique type excel peut faire ça? (somme double, bornes variables, puis finalement afficher le résultat sous forme d'équation en fonction de x et y et non un réel)
Bonjour,
@Laos
essaies de comprendre c'est quoi la double somme telle qu'elle est écrite (Ne l n'éclates surtout pas en 2), tu verras qu'il y a des réponses que tu peux toi-même apporter
C'est un détail technique, si , on prendra
, on prendra 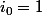 et si
et si  ,
,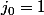
après avoir éclater la somme chose à ne faire.!!!!!!!!
et n'essaies pas de permuter les deux sommes.
On n'a pas a calculer des sommes de séries mais des sommes finies
L'indice est assujetti à varier pour
est assujetti à varier pour  donné entre
donné entre 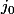 et
et  et comme il est entier entre
et comme il est entier entre 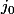 et
et =E(400/i)) et la somme
et la somme ) devient
devient ) et n'a de sens que si
et n'a de sens que si 
@Laos
La somme devient donc
essaies de comprendre c'est quoi la double somme telle qu'elle est écrite (Ne l n'éclates surtout pas en 2), tu verras qu'il y a des réponses que tu peux toi-même apporter
Ce sont bien à la fois bornes et indices qui sont multiples de 5, par contre i et j ne peuvent prendre des valeurs négatives ni nulles.
C'est un détail technique, si
après avoir éclater la somme, on se retrouve avecqui n'est pas "calculable"...
après avoir éclater la somme chose à ne faire.!!!!!!!!
et n'essaies pas de permuter les deux sommes.
qui n'est pas "calculable"
On n'a pas a calculer des sommes de séries mais des sommes finies
L'indice
deltab a écrit:
essaies de comprendre c'est quoi la double somme telle qu'elle est écrite (Ne l n'éclates surtout pas en 2), tu verras qu'il y a des réponses que tu peux toi-même apporter
après avoir éclater la somme chose à ne faire.!!!!!!!!
et n'essaies pas de permuter les deux sommes.
Du coup j'ai essayé de l'écrire sous forme développée (ensemble des combinaisons i*j) :
Ce qu'on remarque c'est que le dernier terme s'annule, on peut donc arrêter la borne de j à l'avant dernier terme
On voit aussi apparaître la somme des 1 mais tu m'as déconseillé de scinder la somme donc cette observation ne me sert à rien...
Les intervalles de i et j étant centrés sur 20 (même si ça n'est pas tout à fait centré pour j), alors forcément les intervalles de i et j se recoupent, faisant apparaître des doublons dans la somme mais je ne sais pas les faire apparaître et surtout pas sûre que ce soit utile...
J'ai essayé d'encadrer la somme en partant de
En résumé j'ai besoin d'un indice!! :happy2:
[quote="Laos"]Du coup j'ai essayé de l'écrire sous forme développée (ensemble des combinaisons i*j) :
 [/QUOTE
[/QUOTE
Que désigne pour toi les , etc...
, etc...
Tu risques de t'embrouiller car le produit ij est assujetti à à varier entre et 400 vu que le problème: trouver tous les couples d'entiers
et 400 vu que le problème: trouver tous les couples d'entiers ) tels
tels 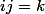 , où
, où  n'est pas simple à résoudre, ne rend pas pas la somme plus simple à calculer.
n'est pas simple à résoudre, ne rend pas pas la somme plus simple à calculer.
Le fait que certains termes s'annulent provient du fait que si est entier, il est égale à sa partie entière, la dernière valeur valeur
est entier, il est égale à sa partie entière, la dernière valeur valeur ) de
de  sera égale à
sera égale à  et
et = i \times \frac{400}{i}=400) et
et 
Exemples:
Pour=20) et
et 
mais pour=21) et
et  .
.
On aurait pu éliminer ces termes nuls en prenant=E(\frac{400}{i})) sauf si
sauf si  entier et dans ce cas prendre
entier et dans ce cas prendre =\frac{400}{i}-1=E(\frac{400}{i})-1)
Mais est-ce c'était nécessaire?
Que désigne pour toi les
Tu risques de t'embrouiller car le produit ij est assujetti à à varier entre
Le fait que certains termes s'annulent provient du fait que si
Exemples:
Pour
mais pour
On aurait pu éliminer ces termes nuls en prenant
Mais est-ce c'était nécessaire?
Laos a écrit:Ca représente juste la suite de terme i et j sur leurs intervalles respectifs (i1=20-2/5x ; i2=20-2/5x+1 ; i3=20-2/5x+2 ;...;in=20+2/5x)
Mais cette somme est-elle vraiment résolvable? As-tu une solution?
Qu'entends-tu par résolvable?
Tu as un petit problème de notation.
Pour moi
Pour toi,
Du coup j'ai essayé de l'écrire sous forme développée (ensemble des combinaisons i*j) :
1-\frac{i_0j_0}{400}+1-\frac{i_0j_1}{400}+1-\frac{i_0j_2}{400}+...+0+1-\frac{i_1j_0}{400}+1-\frac{i_1j_1}{400}+1-\frac{i_1j_2}{400}+...+0+1-\frac{i_2j_0}{400}+1-\frac{i_2j_1}{400}+1-\frac{i_2j_2}{400}+...+0+...
x et y étant donnés, on commence en premier par trouver les 2 bornes que j'ai notées i_0 et i_1.
Comme ij 20-2y/5 ,(20-2/5y prête à confusion) et le minimum des valeurs A->20+y/5 et B=400/i, A est imposé dans la 1ére somme écrite et la 2ème provient de 1-ij/400 >0.
et fais un effort pour comprendre!
Bonjour.
Je vais te donner sous forme algorithmique la méthode de calcul de la somme
+1<span style=) .................(valeur entière la plus proche)
.................(valeur entière la plus proche)
X1=20+2x/5
I_1=E(X1) ..................................................(valeur entière approchée par défaut de X1)
Si X1-E(X1)>0.5, I_1=E(X1)+1.......................(valeur entière la plus proche)
Y0=20-2y/5
J_0=E(Y0) ..................................................(valeur entière approchée par défaut de Y01)
Si J_00.5, J_0=E(Y0)+1.................(valeur entière la plus proche)
Y1=20+y/5
A=E(Y1) ..................................................(valeur entière approchée par défaut de Y1)
Si Y1-E(Y1)>0.5, A=E(Y1)+1.......................(valeur entière la plus proche)
* on aura besoin ce cette valeur pour calculer J_1(i) la somme [quote]\sum_{j_0 \le j \le j_1,ij= J_0
Faire pour j variant de J_0 à J_1
S = S +(1-(ij/400))
[COLOR=Blue]*sinon la somme [TEX] \sum_{j_0 \le j \le j_1,ij<400} \text{ } \left( 1-\frac{ij}{400} \right)"/> n'a aucun sens (somme vide)
4) Tenir compte du facteur PR
S = PR x S
Remarque:
Les lignes commençant par (*) même en retrait sont des commentaires de même pour ce qui suit des points de suspension, tiens, je vais reprendre et écrire les commentaires en bleu
Il est clair que je n'ai pas écrit un algorithme mais une forme algorithmique pouvant être transcrite en terme d'algorithme (syntaxe et vocabulaire (commande, instruction)) ou directement transcrite dans un langage de programmation
OUF!, ça a été long d'écrire
Je vais te donner sous forme algorithmique la méthode de calcul de la somme
X1=20+2x/5
I_1=E(X1) ..................................................(valeur entière approchée par défaut de X1)
Si X1-E(X1)>0.5, I_1=E(X1)+1.......................(valeur entière la plus proche)
Y0=20-2y/5
J_0=E(Y0) ..................................................(valeur entière approchée par défaut de Y01)
Si J_00.5, J_0=E(Y0)+1.................(valeur entière la plus proche)
Y1=20+y/5
A=E(Y1) ..................................................(valeur entière approchée par défaut de Y1)
Si Y1-E(Y1)>0.5, A=E(Y1)+1.......................(valeur entière la plus proche)
* on aura besoin ce cette valeur pour calculer J_1(i) la somme [quote]\sum_{j_0 \le j \le j_1,ij= J_0
Faire pour j variant de J_0 à J_1
S = S +(1-(ij/400))
[COLOR=Blue]*sinon la somme [TEX] \sum_{j_0 \le j \le j_1,ij<400} \text{ } \left( 1-\frac{ij}{400} \right)"/> n'a aucun sens (somme vide)
4) Tenir compte du facteur PR
S = PR x S
Remarque:
Les lignes commençant par (*) même en retrait sont des commentaires de même pour ce qui suit des points de suspension, tiens, je vais reprendre et écrire les commentaires en bleu
Il est clair que je n'ai pas écrit un algorithme mais une forme algorithmique pouvant être transcrite en terme d'algorithme (syntaxe et vocabulaire (commande, instruction)) ou directement transcrite dans un langage de programmation
OUF!, ça a été long d'écrire
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
