Soit la suite définie par x0=1 et x(n+1)=ln(exp(xn)-xn). J'ai prouvé que la suite est positive et converge vers 0 en décroissant, puis (par d'Alembert) que la série sigma des xn converge.
Je dois maintenant calculer la somme des xn pour n=0 à l'infini, et je sèche ...
Avez-vous des idées ? Merci d'avance.
Somme des termes d'une suite définie par récurrence
3 messages
- Page 1 sur 1
Re: Somme des termes d'une suite définie par récurrence
par Ben314 » 07 Jan 2019, 10:17
Salut,
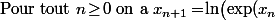\!-\!x_n\big)\text{ donc }x_n\!=\!\exp(x_n)\!-\!\exp(x_{n+1})\text{ et on en d\'eduit que}\cr\sum_{k=0}^{n}\!x_k=\exp(x_0)\!-\!\exp(x_{n+1})\ \mathop{\longrightarrow}\limits_{n\to\infty}\ \exp(x_0)\!-\!\exp(0)=e\!-\!1)
.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Somme des termes d'une suite définie par récurrence
par BenoîtL-21 » 07 Jan 2019, 11:23
Merci Ben314 !!
Bordel, comment n'y ai-je pas pensé ? Quelle chèvre !!
Bonne journée.
Bordel, comment n'y ai-je pas pensé ? Quelle chèvre !!
Bonne journée.
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :