Incompatibilité, notion ensembliste ou probabiliste ?

[Pseuda]

Bonsoir,

Dernière tentative.

1ère solution (l'officielle) : on définit l'indépendance par P(A inter B) = P(A)*P(B), et on définit la probabilité conditionnelle de P(A sachant B) quand P(B)0 par P(A sachant B) = P(A inter B) / P(B).

2ème solution (la plus intuitive pour certains) : on définit la probabilité conditionnelle de P(A sachant B) pour P(B)0 par P(A sachant B) = P(A inter B) / P(B), et on dit que A et B sont indépendants si P(B)0 et P(A) = P(A sachant B) ou si P(A)0 et P(B) = P(B sachant A), ou si P(A)=P(B)=0.

Un choix a été fait. Personnellement, je préfère la 1ère (plus simple). Avec ce choix, on a immédiatement que A et B sont indépendants ssi P(A sachant B) = P(A) (sauf cas triviaux).

(Tout ceci me fait me rendre compte de l'intérêt d'avoir séparé l'univers de ses probabilités : pour un même univers, on manipule plusieurs probabilités en parallèle.)

[beagle]

la dernière?
perso je ne suis ni dans 1 ni dans 2, on parle de mélanger, de présenter, d'amener à

par contre la 1 sèche d'emblée est assez horrible

avec les explications qui expliquent indépendance et lié on retrouve si on les a perdu, ou on consolide la définition du 1 d'un : ben oui quoi!Bref des connaissances qui sont en réseau, du solide.

alors que la solution 1 d'emblée on accepte la définition , on la subit et elle s'éclairera (peut-être? et la preuve est faite à mon avis sur ce fil) un jour.Avec des types qui appliquent sans savoir pourquoi ils ont raison, ils ont démontré l'indépendance avec la définition et la formule, mais ne savent pas de quoi il s'agit,
et d'autres qui apprennent la formule:
p(A inter B) = p(A sachant B) / p(A)
ah non c'est /p(B)
ben dommage ça se lit sur une patate, bref la définition est comme le port salut, c'est écrit dessus (sur la patate).

[zygomatique]

il faut bien comprendre que parler de probabilité conditionnelle c'est simplement changer d'univers


si U est un univers probabilisé et A et B deux parties de U alors les événements A et B sont indépendants : .................................... épictou

mais évidemment donner un sens à cette relation, s'en donner une image, une vision n'est pas forcément évident ...


maintenant (en supposant que ) regardons ce qui se passe dans l'univers A

de la probabilité P on déduit la probabilité Q par : pour toute partie B de U :

alors Q est une probabilité définie sur l'univers A car toute partie de A est la trace d'une partie de U

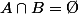
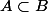
en particulier si alors Q(B) = 0 et si alors Q(B) = Q(A) = 1

alors dire que A et B sont indépendants signifie que Q(B) = P(B) : réaliser ou non A n'influe pas sur la réalisation de B

ou encore la probabilité de réaliser B dans U est la même que la probabilité de réaliser B (inter A) dans A

il est alors naturel de considérer / mesurer comment influe la réalisation de A sur la réalisation de B ... ou encore qu'est-ce que ça signifie que ?

et on tombe naturellement sur la probabilité conditionnelle de B sachant A ... qui mesure l'influence qu'a la réalisation de A sur la réalisation de B

enfin voila ""ma vision"" des choses ....

[beagle]

"faut bien comprendre que parler de probabilité conditionnelle c'est simplement changer d'univers"
ouf!


"si U est un univers probabilisé et A et B deux parties de U alors les événements A et B sont indépendants : .................................... épictou

mais évidemment donner un sens à cette relation, s'en donner une image, une vision n'est pas forcément évident ..."
alors que l'inverse parait plus logique, indépendant et lié sont le sens, et permettent la vision , ainsi que les formules.C'est vraiment là où vous m'étonnez.

[beagle]

Voilà un exemple de probas liées et indépendantes.
Et les limites de la définition mathématique épicetou.
Définition bien utile ce n'est pas le problème.
Mais définition qui ne peut pas correspondre à des évènements jaunes.
L'indépendance ou la liaison lorsqu'elle préexiste, c'est elle qui donne et fait les calculs.
ce ne sont pas les calculs qui disent indépendance grace à la formule définition.

un exemple ici:
superieur/probabilites-liees-independantes-encore-t185563.html#p1231697

[Dlzlogic]

Bonsoir,
J'avoue que j'ai été un peu surpris de lire la définition de l'indépendance : "on définit l'indépendance par P(A inter B) = P(A)*P(B)". Pour moi, ce serait plutôt "si deux variables sont indépendantes, alors P(A inter B) = P(A)*P(B)".
D'autre part, on démontre rigoureusement que la "combinaison la plus probable est celle qui correspond à la réalisation des piles et faces en nombre égaux" (voir cours de Lévy).

[beagle]

Bonsoir,
J'avoue que j'ai été un peu surpris de lire la définition de l'indépendance : "on définit l'indépendance par P(A inter B) = P(A)*P(B)". Pour moi, ce serait plutôt "si deux variables sont indépendantes, alors P(A inter B) = P(A)*P(B)".
D'autre part, on démontre rigoureusement que la "combinaison la plus probable est celle qui correspond à la réalisation des piles et faces en nombre égaux" (voir cours de Lévy).

Il faut les deux en fait.
La définition telle que donnée.C'est le plus rigoureux.
Bien que le p sachant l'un égale le p QS est tout aussi rigoureux et plus parlant.Il est moins concis et gène quand proba nulle division par zéro.
On fait les calculs ce la se vérifie alors indépendance, cela ne vérifie pas alors pas indépendance.


Mais il faut bien pouvoir faire le chemin inverse.C'est indépendant donc le calcul.
Le hic c'est de faire comme moi et de dire c'est indépendant donc
et en fait c'était des probas liées.
Là ce n'est pas rigoureux, tu dis c'est indépendant car, mais ce n'est pas une démonstration mathématique.
Mais sans autre défintion de indépendance ou lié, c'est bien difficile de manipuler des exos type cela sera indépendant quand ceci cel ou cela sera lié si je modifie cela.Il ya bien là une notion qui a besoin aussi de sa définition.Et heureusement cela colle avec le français pour une fois, donc dommage de bouder ce plaisir qu'un nom corresponde bien.

[Dlzlogic]

Pour le fun, voici la démonstration:

Soit a le nombre de cas favorables à la production de A et b celui des cas favorables à l'évènement B. On a :
P(A) = a/M ; P(B) = b/N.
Le nombre total de cas possibles est égal à M x N, puisque, par suite de l'indépendance, à toute éventualité M peuvent être associées chacune des éventualités N.
De même le nombre de cas favorables à l'évènement (A + B) est a x b puisque l'évènement gagnant ne peut être réalisé qu'en associant l'un quelconque des a cas favorables à A avec l'un quelconque des b cas favorables à B. Par suite :
P(A + B) = (a x b)/(M x N) = a/M x b/N = P(A) x P(B).

[beagle]

Bonjour mesdames et bonjour messieurs.
Tous les intervenants de fil de discussion sont amicalement invités à répondre sur le fil ci après:
superieur/probabilites-liees-independantes-encore-t185563-40.html

Pour Dlzlogic, je vais faire tourner les tables puisqu'il s'est fait descendre.

[beagle]

Bonjour Skullkid,
pourrais-tu répondre au fil de discussion mis sus-jaccent,
possibilité de répondre uniquement à la question 6) pour ne pas avoir de calcul à faire,
mais une réponse mathématique, sachant que tu ne réponds sur ce sujet que pour faire des maths.Donc juste comme cela, la question est :comment rédiges-tu une réponse à la 6).

La même question s'adresse à zygomatique et pseuda , dès lors qu'ils seraient présents sur le site.
Les autres personnes peuvent répondre également bien sur.