Problème ensembliste
24 messages
- Page 1 sur 2 - 1, 2
Problème ensembliste
Bonjour
Je dois démontrer plusieurs propriétés avec P(E). La première est la suivante:
Quelle relation entre P(EUF) et P(E) U P(F)
J'en ai d'autres, mais je ne comprend pas, quels sont les changements dans le raisonnement par rapport à quand on démontre des relations entre des ensembles.
Ex: montrer que E inclus dans F si ....
Je pensais partir du fait que P(EUF) avec E contient x éléments er F contient y éléments = 2^(x+y) éléments.
Pouvez vous m'orienter un peu? Dans le cours, nous n'avons aucune formule avec P(E) mis à part 2^n.
Merci
Je dois démontrer plusieurs propriétés avec P(E). La première est la suivante:
Quelle relation entre P(EUF) et P(E) U P(F)
J'en ai d'autres, mais je ne comprend pas, quels sont les changements dans le raisonnement par rapport à quand on démontre des relations entre des ensembles.
Ex: montrer que E inclus dans F si ....
Je pensais partir du fait que P(EUF) avec E contient x éléments er F contient y éléments = 2^(x+y) éléments.
Pouvez vous m'orienter un peu? Dans le cours, nous n'avons aucune formule avec P(E) mis à part 2^n.
Merci
Re: Problème ensembliste
Bonjour,
Pour la première propriété, l'inclusion\cup\mathcal{P}(F)\subset\mathcal{P}(E\cup F)) est immédiate.
est immédiate.
L'autre inclusion est fausse en général, comme le montre l'exemple et la partie
et la partie  qui n'est ni dans
qui n'est ni dans  ni dans
ni dans  .
.
Au passage, la formule=2^{\mathrm{Card }E}) dans le cas où
dans le cas où  est fini montre le résultat ci-dessus si tu l'appliques à deux ensembles finis disjoints (puisqu'en général
est fini montre le résultat ci-dessus si tu l'appliques à deux ensembles finis disjoints (puisqu'en général  ).
).
Pour la première propriété, l'inclusion
L'autre inclusion est fausse en général, comme le montre l'exemple
Au passage, la formule
Re: Problème ensembliste
Que veut dire "l'inverse" ?
Essaie de t'exprimer précisément, ça te sera bénéfique.
Essaie de t'exprimer précisément, ça te sera bénéfique.
Re: Problème ensembliste
Soient E{1,2,3,4} et F{3,4,5,6}
P(EnF) = {3,4} inclus dans E ET dans F.
Par contre, Ni E, Ni F, sont inclus dans (EnF).
De manière générale, la seule possibilité pour que il y ait la double inclusion est que E et F soient un meme ensemble.
P(EnF) = {3,4} inclus dans E ET dans F.
Par contre, Ni E, Ni F, sont inclus dans (EnF).
De manière générale, la seule possibilité pour que il y ait la double inclusion est que E et F soient un meme ensemble.
Re: Problème ensembliste
Tu t'es trompé : tu as écrit 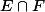 , par
, par ) .
.
Ne fais pas la confusion entre un ensemble et l'ensemble de ses parties !
) : l'ensemble des ensembles contenus dans
: l'ensemble des ensembles contenus dans 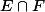 .
.
 \cap \mathcal{P}( F)) : l'ensemble des ensembles qui sont à la fois contenus dans
: l'ensemble des ensembles qui sont à la fois contenus dans  et contenus dans
et contenus dans  .
.
Ne fais pas la confusion entre un ensemble et l'ensemble de ses parties !
Re: Problème ensembliste
Soient E ={1,2,3,4} et F ={3,4,5,6}
P(EnF) = {3,4} inclus dans P(E) ET dans P(F).
Par contre, Ni P(E), Ni P(F), sont inclus dans P(EnF).
De manière générale, la seule possibilité pour que il y ait la double inclusion est que E et F soient un meme ensemble.
La c'est bon?
P(EnF) = {3,4} inclus dans P(E) ET dans P(F).
Par contre, Ni P(E), Ni P(F), sont inclus dans P(EnF).
De manière générale, la seule possibilité pour que il y ait la double inclusion est que E et F soient un meme ensemble.
La c'est bon?
Re: Problème ensembliste
Non, pas du tout bon.
Lis-tu ce que j'écris ?
Tu ne fais toujours pas la différence entre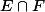 (l'ensemble des éléments qui appartiennent à la fois à
(l'ensemble des éléments qui appartiennent à la fois à  et à
et à  ) et
) et ) (l'ensemble des ensembles qui sont contenus dans
(l'ensemble des ensembles qui sont contenus dans 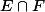 ). Dans ton exemple:
). Dans ton exemple:

=\{\emptyset, \{3\},\{4\},\{3,4\}\})
Lis-tu ce que j'écris ?
Tu ne fais toujours pas la différence entre
Re: Problème ensembliste
Excuse moi, j'avais pas compris, je pensais que tu parlais de ma manière d'écrire ma réponse !!
Ok j'ai compris la différence.
Par contre, la réponse finale est la même du coup, non? C'est à dire que il n'y a pas double inclusion, et que seul P(EnF) c P(E) n P(F) ?
Merci en tout cas !!
J'ai peut être du mal à matérialiser P(E) n P(F)
Ok j'ai compris la différence.
Par contre, la réponse finale est la même du coup, non? C'est à dire que il n'y a pas double inclusion, et que seul P(EnF) c P(E) n P(F) ?
Merci en tout cas !!
J'ai peut être du mal à matérialiser P(E) n P(F)

Re: Problème ensembliste
Abilys38 a écrit:Par contre, la réponse finale est la même du coup, non? C'est à dire que il n'y a pas double inclusion, et que seul P(EnF) c P(E) n P(F) ?
Non tu te trompes. Relis soigneusement mes messages.
Re: Problème ensembliste
Ok je reviendrai avec une réponse quand Jaurai une feuille et un stylo ce sera plus simple !!
Re: Problème ensembliste
E = {1, 2, 3}
F = {2,3, 4}
EnF = {2,3}
A partir de la:
P(E) = {0,1,2, 3,12, 13, 23, 123} et
P(F) = {0, 2,3,4,23,24,34,234}
P(EnF) = {0, 2, 3, 23} basé sur EnF
P(E) n P(F) = {0, 2, 3, 23} basé sur P(E) et P(F)
Il y a donc double inclusion (égalité)?
F = {2,3, 4}
EnF = {2,3}
A partir de la:
P(E) = {0,1,2, 3,12, 13, 23, 123} et
P(F) = {0, 2,3,4,23,24,34,234}
P(EnF) = {0, 2, 3, 23} basé sur EnF
P(E) n P(F) = {0, 2, 3, 23} basé sur P(E) et P(F)
Il y a donc double inclusion (égalité)?
Re: Problème ensembliste
Il y a du progrès mais :
1°) Tes écritures sont incorrectes. Il manque les accolades, etc.
2°) Un exemple n'est pas une démonstration (démonstration qui n'est pas compliquée)
1°) Tes écritures sont incorrectes. Il manque les accolades, etc.
2°) Un exemple n'est pas une démonstration (démonstration qui n'est pas compliquée)
Re: Problème ensembliste
1) ok je ferai attention a ca
2) ok je vais réfléchir à la démonstration. Mais j'avais besoin de comprendre le mécanisme avant.
2) ok je vais réfléchir à la démonstration. Mais j'avais besoin de comprendre le mécanisme avant.
Re: Problème ensembliste
Soit n le nombre d'éléments communs à E et F. P(EnF) = 2^n
Par ailleurs, P(E) n P(F) correspond aux nombres de sous parties communes à P(E) et P(F) soit exactement les mêmes sous parties que pour P(EnF). Ainsi:
P(EnF) = P(E) n P(F)
Par ailleurs, P(E) n P(F) correspond aux nombres de sous parties communes à P(E) et P(F) soit exactement les mêmes sous parties que pour P(EnF). Ainsi:
P(EnF) = P(E) n P(F)
Re: Problème ensembliste
Bonjour,
Attention à la définition de) , il s'agit d'un ensemble et non d'un nombre. Donc quand on dit que
, il s'agit d'un ensemble et non d'un nombre. Donc quand on dit que =\mathcal{P}(E)\cap\mathcal{P}(F)) , il s'agit d'une égalité d'ensemble, au sens où il y a une double inclusion entre les deux.
, il s'agit d'une égalité d'ensemble, au sens où il y a une double inclusion entre les deux.
D'ailleurs, tu sembles mélanger nombre et ensemble dans ta rédaction.
Au passage, ta rédaction laisse penser que tu dis :
• Soit que "les deux ensembles ont le même nombre d'éléments donc ils sont égaux
• Soit que tes deux ensembles sont égaux parce qu'ils ont les mêmes éléments, ce qui est LA chose à démontrer ici (ce que tu ne fais pas ici puisque tu dis qu'ils sont égaux parce qu'ils sont égaux ).
).
Ici, tu veux montrer une égalité d'ensembles. Procèdes donc par double inclusion :
• D'abord, montres que\subset\mathcal{P}(E)\cap\mathcal{P}(F))
• Ensuite, montres que\cap\mathcal{P}(F)\subset\mathcal{P}(E\cap F))
Puis pour montrer que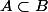 , c'est classique :
, c'est classique :
"Soit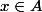 . Alors [...] Donc
. Alors [...] Donc 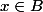 ."
."
Le [...] va dépendre des propriétés de et
et  .
.
Attention à la définition de
D'ailleurs, tu sembles mélanger nombre et ensemble dans ta rédaction.
Au passage, ta rédaction laisse penser que tu dis :
• Soit que "les deux ensembles ont le même nombre d'éléments donc ils sont égaux
• Soit que tes deux ensembles sont égaux parce qu'ils ont les mêmes éléments, ce qui est LA chose à démontrer ici (ce que tu ne fais pas ici puisque tu dis qu'ils sont égaux parce qu'ils sont égaux
Ici, tu veux montrer une égalité d'ensembles. Procèdes donc par double inclusion :
• D'abord, montres que
• Ensuite, montres que
Puis pour montrer que
"Soit
Le [...] va dépendre des propriétés de
Re: Problème ensembliste
Justement, pour des ensembles, je procède avec x appartient ...
Mais avec des sous ensemble, je ne sais pas trop comment faire. J'étais habitué à démontrer des inclusions avec de simples ensembles et non avec des parties.
Je sais comment prouver que A c B mais prouver ce que je dois prouver ici, c'est une autre histoire
Mais avec des sous ensemble, je ne sais pas trop comment faire. J'étais habitué à démontrer des inclusions avec de simples ensembles et non avec des parties.
Je sais comment prouver que A c B mais prouver ce que je dois prouver ici, c'est une autre histoire

Re: Problème ensembliste
L'idée ici est que le  dont tu parles est un ensemble.
dont tu parles est un ensemble.
Robot t'as déjà expliqué ce qu'étaient) et
et \cap \mathcal{P}(F)) :
:
Demandes-toi alors : si je prends un ensemble contenu dans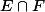 , est-ce qu'il est contenu à la fois dans
, est-ce qu'il est contenu à la fois dans  et dans
et dans  ? Et réciproquement ?
? Et réciproquement ?
La démonstration devrait alors venir d'elle-même
Robot t'as déjà expliqué ce qu'étaient
Robot a écrit:: l'ensemble des ensembles contenus dans
.
: l'ensemble des ensembles qui sont à la fois contenus dans
et contenus dans
.
Demandes-toi alors : si je prends un ensemble contenu dans
La démonstration devrait alors venir d'elle-même
Re: Problème ensembliste
Ok je vais essayer, merci. Et comment appelles tu un ensemble lambda? (C'est à dire au lieu de x)
24 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

