Equation ensembliste
78 messages
- Page 2 sur 4 - 1, 2, 3, 4
exemple:dans le plan
deux droites d1 et d2 sont sécantes en A.
d3 n'est pas // à d1 ni à d2, et coupe d1 en B, et d2 en C
On appelle E l'ensembles des points A, B, C
Ben, il ne me semble pas grave que dans le cas de 3 droites concourantes A=B=C,
et que l'ensemble E devienne un ensemble à 1 élément.
Enfin je n'en sais rien.
pour les puristes, il conviendrait d'écrire quoi?
deux droites d1 et d2 sont sécantes en A.
d3 n'est pas // à d1 ni à d2, et coupe d1 en B, et d2 en C
On appelle E l'ensembles des points A, B, C
Ben, il ne me semble pas grave que dans le cas de 3 droites concourantes A=B=C,
et que l'ensemble E devienne un ensemble à 1 élément.
Enfin je n'en sais rien.
pour les puristes, il conviendrait d'écrire quoi?
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
beagle a écrit:C'était mon sentiment au départ, on a le droit d'écrire 4 éléments d'un ensemble qui n'en comporte que 2???
Maintenant si a, b, c, d sont comme dans l'exemple de géométrie que j'ai mis en exemple, des éléments très généralistes, "normalement" distincts, sauf dans les cas particuliers de calculs où ils ne le sont plus, la notation me semble plausible.
dans mon exo un ensemble est constitué des quatre points A, B, C, D,
mais ces points sont des variables qui dans certains cas vont se confondre.
Je ne vois pas comment serait noté de façon générale l'ensemble de points décrivant la figure géométrique générale.
L'ensemble en question a au plus 4 éléments et non pas a 4 éléments, nuance.
Le livre étant ancien, il faut consulter le livre lui-même pour la signification de la notation sinon un des livres de cours (de terminale C, D ou E si possible) de la même époque.
deltab a écrit:L'ensemble en question a au plus 4 éléments et non pas a 4 éléments, nuance.
je ne fais pas dans la nuance avoir 4 éléments dont deux sont identiques est avoir 3 éléments.
Tu n'as pas répondu sur le fond j'écris un ensemble de 4 points A, B, C, D,
alors que dans certaines circonstances A peut-ètre égal à B.
cela est choquant oui ou non,
et si oui quelle écriture proposez-vous.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
beagle a écrit:je ne fais pas dans la nuance avoir 4 éléments dont deux sont identiques est avoir 3 éléments.
Tu n'as pas répondu sur le fond j'écris un ensemble de 4 points A, B, C, D,
alors que dans certaines circonstances A peut-ètre égal à B.
cela est choquant oui ou non,
et si oui quelle écriture proposez-vous.
Relis mon précédent message, je viens de le modifier, tu as peut-être la 1ère version. Si l'on se place dans le général, hors contexte de l'exercice, que veut dire pour toi un ensemble de n éléments.
deltab a écrit:Relis mon précédent message, je viens de le modifier, tu as peut-être la 1ère version. Si l'on se place dans le général, hors contexte de l'exercice, que veut dire pour toi un ensemble de n éléments.
il me semble savoir ce qu'est un ensemble de n éléments.
maintenant s'il s'agit de dire que dans le temps on pouvait écrire le problème , très clair et très précis, le problème géométrique que j'ai décrit QS,
s'il s'agit de dire que l'on pouvait écrire l'ensemble des points A, B, et C,
avec comme pas grave du tout qu'un jour , au cas particulier de A=B=C, l'ensemble devient à 1 élément,
et qu'aujourd'hui on n'est plus autorisé à accepter de telles notations,
ben c'est que c'était mieux avant,
comme pour l'excès de rigueur de implication n'est pas démonstration qui nuit de nos jours l'expression plutot que cela n'apporte.
sauf à me dire quelle écriture autorisée à mon problème est de nos jours acceptée , acceptable,...
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Alors recommençons autrement.
On prend a, b, c, d ,e ,f dans les nombres entiers de 1 à 100
On note A l'ensemble a, b , c , d
on note B l'ensemble d, e , f
quand a-t-on A= B?
Ben par exemple quand on a tiré un truc comme a=b=c=d=e=f
alors l'ensemble A ne comprend qu'un seul élément, comme B, et c'est le mème,
les deux ensembles sont égaux.
donc je comprends bien que l'ensemble A avec ses 4 éléments donc de cardinalité 4,
devient de façon choquante un ensemble à 1 seul élément de cardinalité 1.
ben il semblerait que dans le temps, on pouvait ranger tout ensemble, les a,b,c,d et enlever les doublons ensuite,
sans troubler les pères la rigueur.
Tout ceci n'est-il que conventions d'écritures?????
et si oui, quelle convention d'écriture utilisez-vous pour appeler l'ensemble a,b,c,d non encore rangé et dépoussiéré de ses doublons?
On prend a, b, c, d ,e ,f dans les nombres entiers de 1 à 100
On note A l'ensemble a, b , c , d
on note B l'ensemble d, e , f
quand a-t-on A= B?
Ben par exemple quand on a tiré un truc comme a=b=c=d=e=f
alors l'ensemble A ne comprend qu'un seul élément, comme B, et c'est le mème,
les deux ensembles sont égaux.
donc je comprends bien que l'ensemble A avec ses 4 éléments donc de cardinalité 4,
devient de façon choquante un ensemble à 1 seul élément de cardinalité 1.
ben il semblerait que dans le temps, on pouvait ranger tout ensemble, les a,b,c,d et enlever les doublons ensuite,
sans troubler les pères la rigueur.
Tout ceci n'est-il que conventions d'écritures?????
et si oui, quelle convention d'écriture utilisez-vous pour appeler l'ensemble a,b,c,d non encore rangé et dépoussiéré de ses doublons?
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
beagle a écrit:il me semble savoir ce qu'est un ensemble de n éléments.
La question que je t'avais posé concernant "un ensemble de n éléments" n'était pas pour te vexer, loin de là, mais pour qu'on soit sur la même longueur d'ondes. Pour moi un ensemble de n éléments exclut la répétition, pour inclure la répétition, je dirais un ensemble d'au plus n éléments.
Je viens de voir sur internet le problème de notation d'un ensemble par extension, dans Wiki, la répétition est acceptée, dans d'autres sites, on n'en parle pas et les exemples donnés sont sans répétition.
Le problème est qu'un abus de notations peut devenir à la longue la notation.
bonsoir deltab,
je te présente d'abord mes excuses pour le ton, jm'a énervé pour rien.
Ce d'autant que comme je te l'ai dit initialement j'ai été surpris initialement, car les utilisations des ensembles vues sur ce forum m'orientaient sur une utilisation sans répétition effectivement.
Ensuite sur le nombre d'éléments cela ne me semblait pas ma priorité dans la discussion à ce moment là,
car encore une fois quand a,b,c,d peuvent arriver avec a=c, ben pour le moment je ne suis pas focalisé sur la cardinalité de l'ensemble.
Bon, on est sur le forum supérieur et il est normal que vous repreniez pour que les écritures soient rigoureuses.Mais cette rigueur, j'aime la comprendre = ok, bon, ben alors comment je fais pour présenter mon truc, quelles solutions d'écriture remplacent.
je te présente d'abord mes excuses pour le ton, jm'a énervé pour rien.
Ce d'autant que comme je te l'ai dit initialement j'ai été surpris initialement, car les utilisations des ensembles vues sur ce forum m'orientaient sur une utilisation sans répétition effectivement.
Ensuite sur le nombre d'éléments cela ne me semblait pas ma priorité dans la discussion à ce moment là,
car encore une fois quand a,b,c,d peuvent arriver avec a=c, ben pour le moment je ne suis pas focalisé sur la cardinalité de l'ensemble.
Bon, on est sur le forum supérieur et il est normal que vous repreniez pour que les écritures soient rigoureuses.Mais cette rigueur, j'aime la comprendre = ok, bon, ben alors comment je fais pour présenter mon truc, quelles solutions d'écriture remplacent.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
beagle a écrit:bonsoir deltab,
je te présente d'abord mes excuses pour le ton, jm'a énervé pour rien.
Ce d'autant que comme je te l'ai dit initialement j'ai été surpris initialement, car les utilisations des ensembles vues sur ce forum m'orientaient sur une utilisation sans répétition effectivement.
1) Tu n'as pas à t'excuser.
2) Moi-même y compris. C'est pour ça que j'avais ajouté:
Le problème est qu'un abus de notations peut devenir à la longue LA notation.
beagle a écrit:merci chan79,
c'est pas la version wikipedia de 1975 des fois? :lol3:
bon , alors on se fait ch..r pour rien depuis cet après-midi, non?
disons que je ne vois pas trop la logique de cet exo ... qui pourtant date de 75 ..... mise à part pointer la cardinalité nécessaire à l'égalité de deux ensembles ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Cet exo apprend ce qu'est un ensemble.
Un ensemble est une collection.
Deux collections sont identiques lorsqu'elles possèdent les mèmes éléments.
Les doublons, triplets,...ne comptent pas dans cette égalité.
Ils doivent ètre échangés pendant la récréation.
Ensuite la discussion a dérivé sur l'intérèt de mettre tous les éléments collectionnés dans les parenthèses ou de ne mettre qu'un seul exemplaire du mème élément.
J'en reste au fait qu'il soit préférable de mettre l'ensemble avec les doublons dans la mesure où je ne connais pas encore qui va potentiellement doublonner.Et qu'il est toujours possible de ranger plus tard.
L'ensemble A est a,b,c entre parenthèses
l'ensemble B est d,e,f
A union B est a,b,c,d,e,f et on le rangera plus tard en a,b,c,f si besoin.
quant à card A union B , ben ce sera card A + card B - card A inter B
donc le jour où un ensemble E sera 1,1,2,2,3,4
ben cet ensemble est l'union de 1,2,3 et de 1,2,4
card de E est 3+3-2
donc tout va bien.
Un ensemble est une collection.
Deux collections sont identiques lorsqu'elles possèdent les mèmes éléments.
Les doublons, triplets,...ne comptent pas dans cette égalité.
Ils doivent ètre échangés pendant la récréation.
Ensuite la discussion a dérivé sur l'intérèt de mettre tous les éléments collectionnés dans les parenthèses ou de ne mettre qu'un seul exemplaire du mème élément.
J'en reste au fait qu'il soit préférable de mettre l'ensemble avec les doublons dans la mesure où je ne connais pas encore qui va potentiellement doublonner.Et qu'il est toujours possible de ranger plus tard.
L'ensemble A est a,b,c entre parenthèses
l'ensemble B est d,e,f
A union B est a,b,c,d,e,f et on le rangera plus tard en a,b,c,f si besoin.
quant à card A union B , ben ce sera card A + card B - card A inter B
donc le jour où un ensemble E sera 1,1,2,2,3,4
ben cet ensemble est l'union de 1,2,3 et de 1,2,4
card de E est 3+3-2
donc tout va bien.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
chan79 a écrit:salut
petite remarque
si on observe {1;2,3;3} et {1;1;2;2;2,3}, on voit que tout élément de l'un est élément de l'autre.
Ca aide à faire accepter l'égalité de ces deux ensembles ...
Bon WE
moi cela me va bien, c'est la collection des 2,1,3
la mème collection,
le mème ensemble.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Allez, quelques solutions:
quel que soit d:
{d;d;d;d}={d;d;d}
et avec d différent de e:
{e;d;d;d}={d;e;e}
{d;e;d;d}={d;e;e}
{d;d;e;d}={d;e;e}
{e;e;d;d}={d;e;e}
{d;e;e;d}={d;e;e}
{e;d;e;d}={d;e;e}
{e;e;e;d}={d;e;e}
{e;d;d;d}={d;d;e}
{d;e;d;d}={d;d;e}
{d;d;e;d}={d;d;e}
{e;e;d;d}={d;d;e}
{d;e;e;d}={d;d;e}
{e;d;e;d}={d;d;e}
{e;e;e;d}={d;d;e}
et c'est pas fini !
quel que soit d:
{d;d;d;d}={d;d;d}
et avec d différent de e:
{e;d;d;d}={d;e;e}
{d;e;d;d}={d;e;e}
{d;d;e;d}={d;e;e}
{e;e;d;d}={d;e;e}
{d;e;e;d}={d;e;e}
{e;d;e;d}={d;e;e}
{e;e;e;d}={d;e;e}
{e;d;d;d}={d;d;e}
{d;e;d;d}={d;d;e}
{d;d;e;d}={d;d;e}
{e;e;d;d}={d;d;e}
{d;e;e;d}={d;d;e}
{e;d;e;d}={d;d;e}
{e;e;e;d}={d;d;e}
et c'est pas fini !
Bonjour.
Finalement, la notation usuelle d'un ensemble par extension est sans répétions, sinon la répétition est effective. A={a,b,c,d} désigne bien un ensemble à 4 éléments de même que A={a,b,c,d,a,b} mais même si a=b, A={a,c,d}={b,c,d}, mais on n'écrira jamais A={a,b,c,d}.
Il y a des cas où cette notion de répétition doit apparaitre. Quand on dit qu'un polynôme de degré non nul
de degré non nul  a
a  racines, chacune étant comptée avec sa mullplicité, (ce qui en gras est ajouté pour lever toute ambigüité,) alors que le nombre d'éléments de l'ensemble des racines de P est
racines, chacune étant comptée avec sa mullplicité, (ce qui en gras est ajouté pour lever toute ambigüité,) alors que le nombre d'éléments de l'ensemble des racines de P est 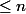 (et
(et 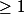 ).
).
beagle a écrit:ben j'avais dit c'est un bel exo de dénombrement,
donc ne m'étonne pas d'y voir chan79 à l'oeuvre,
c'est le genre de truc qu'il aime généralement!
Finalement, la notation usuelle d'un ensemble par extension est sans répétions, sinon la répétition est effective. A={a,b,c,d} désigne bien un ensemble à 4 éléments de même que A={a,b,c,d,a,b} mais même si a=b, A={a,c,d}={b,c,d}, mais on n'écrira jamais A={a,b,c,d}.
Il y a des cas où cette notion de répétition doit apparaitre. Quand on dit qu'un polynôme
78 messages
- Page 2 sur 4 - 1, 2, 3, 4
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

