Ncdk a écrit:Bonjour,
J'ai repris un peu la question en regardant bien les définitions, jespère m'en être un peu mieux sortit qu'auparavant.
Pour
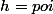
On voit que

et

sont des morphismes d'anneaux, du coup leur composé aussi.
On peut ensuite s'intéresser de plus près à

et

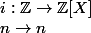
Et
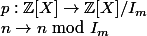
Avec p qui est une application surjective, du fait que c'est une projection canonique.
J'ai essayé de me poser la question suivante :
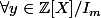
,
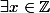
tel que
=y)
?
Je n'arrive pas à trouver de réponse, je dirais oui à condition que

soit une bijection, car on dirait une application constante.
Pour déterminer le
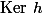
on sait que c'est équivalent à
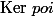
Donc c'est
)=0 \} \Longleftrightarrow \{x \in \mathbb{Z} | p(x)=0 \})
On sait que
=x \text{mod }I_m=0)
ça voudrait dire que
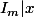
donc que
)
J'arrive tout de même pas à un bon truc, je cherche donc à savoir ou sont les coquilles, les belles coquilles

Oui il y'a quelques coquilles

.
Pour commencer:
 \to P(X) \text{ mod }I_m)
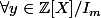
,
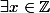
tel que
=y)
?
Oui c'est juste, mais encore? en gros si tu pousses un tout petit peu plus loin la traduction, cela revient à se demander si un élément de
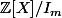
admet un représentant constant. Reponse?
Pour cela, chose que tu aurais du faire depuis longtemps sur cet exo:
Montrer que
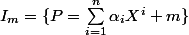
ie ce sont les polynomes dont le terme constant est m. Cela va beaucoup t'aider je pense!
Pour le noyau, t'as écrit une enorme betise.
"On sait que
=x \text{mod }I_m=0)
" ça oui. Mais apres c'est pas du tout ça.
Deja quest ce que ça veut dire
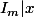
alors que I_m est un idéal de Z[X] et x un entier?...
Tout ce que t'as à dire c'est que
=x \text{mod }I_m=0)
ie
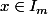
et donc quels sont les entiers qui sont dans I_m?
Dans tout ce que je dis je confonds entier et polynome constant égal à un entier, mais cela doit etre clair que ce n'est pas la même chose
