Après la chose que je comprends pas avec cette histoire d'isomorphisme, c'est un peu les questions que je passe car ça me prend la tête, mais j'aimerai réussir, ça fait cancre ce que je dis :ptdr:
Mais par exemple dans ce cas de figure, j'aimerai bien pouvoir faire un dessin mais je sais pas comment le faire correctement ici, c'est nos profs qui nous habitue à faire des schémas avec nos applications histoire que ça soit lisible et compréhensible.
Je vais expliquer le dessin

On a une application f surjective qui va de A dans B
Ensuite, en partant de B on a une autre application qui est la projection canonique de B dans B/J
Jusque là on a un triangle, et il manque l'application en diagonale donc de A dans B/J qui est la composé de f et projection canonique.
Maintenant, toujours en partant de A, il est nécessaire d'avoir une application qui va de A dans
)
donc qui est la projection canonique elle aussi. Et une application qui va de
)
dans B/J.
Il y a encore une application en diagonale de A dans B/J qui est celle que j'ai dit plus haut et qui au final est aussi la composée de la projection canonique de A dans
)
et l'application qui va de
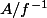
dans B/J.
Mais je trouve pas la logique pour prouver qu'il y a un isomorphisme, il faut prouver que cette application de
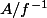
dans B/J soit bijective, mais j'ignore surement les outils à ma disposition pour y arriver, c'est le théorique qu'il y a derrière qui me fait défaut.
Du coup j'ai parfois du mal à vous suivre

