Équation à partir d'une courbe
37 messages
- Page 2 sur 2 - 1, 2
par bartras » 15 Sep 2015, 22:57
ah je crois avoir compris, il faut répliquer trois fois ce que j'ai fais...^^ ça va être long
par alphamethyste » 16 Sep 2015, 00:13
bonjour (oui j'ai dormis mais là c'est bon je suis réveillé)
juste avant que je tape ma fonction dans ma machine
ici j'explique tout en detail et j'ai re-écris ici les fonctions
je viens de voir que dans les images la fonction f4 et sa derivée f'4 était mal écrite une petite erreur d'écriture mais facilement reperable
bon bref tu as trois intervalles fermés [T0;T1],[T1;T2],[T2;T3]
tu t'occupe d'un intervalle puis de l'autre puis de l'autre
par exemple prenons le premier intervalle [T0;T1] , donc oublie les autres et comme apres c'est ce que tu va faire pour les autres intervalles (une fois que tu te sera occupé de celui là ) eh bien tu obtiendra une application de classe C1 (une seule fois derivable sur tout l'intervalle [T0;T3] et d'ailleurs son domaine de definition c'est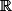
)
)
donc bref alors prenons le premier intervalle [T0;T1]
alors tu pose p1=T0 p2=T1 q1=g(T0) q2=g(T1) q'1=g'(T0) q'2=g'(T1)
g et g' sa derivée étant la fonction que tu recherche (mais que justement tu ne connais pas)
tu te donne tous les autres parametres tu est libre de te les choisir à ta guise comme tu veux
de toute façon tu obtiendra quand même f(p1)=q1,f(p2)=q2,f'(p1)=q'1,f'(p2)=q'2
dans la condition que tes autres parametres respectent ci-dessous :
donc u=1 ou u=-1 que tu choisi comme tu veux
un relatif donc n=-2 ou n=-1 ou n=0 ou n=1 ou n=2 etc ... que tu choisi comme tu veux
PAIR ET NON NUL (donc k=2,k=4 etc ... que tu choisi comme veux )
IMPAIR (donc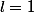 
,
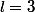etc ... que tu choisi comme tu veux)
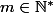donc m=1 ou m=2 etc ... que tu choisi comme tu veux (un entier naturel NON NUL)
donc m1=1 ou m1=2 etc ... que tu choisi comme tu veux (un entier naturel NON NUL)
donc m2=1 ou m2=2 etc ... que tu choisi comme tu veux (un entier naturel NON NUL)
donc un réel comme tu veux tu peut prendre tout aussi bien a=0 ou 
tu est libre!
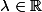selon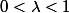 
donc un réel comme tu veux dans l'intervalle ouvert entre zero et un
mais attention choisi les de façon que tu obtienne l'inégalité
-v.sin(2\pi v)\neq 0)
avec au choix tu choisi l'un des deux ci-dessous :
ou bien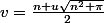
ou bien ^2-\pi}}{2})
puis determine
et vois si cette inégalité est respectée (sinon fais d'autres choix)
___________________________________
une fois que ça c'est fait alors tu pose
___________________________________
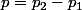
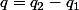
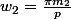
et là tu as tous les parametres pour les appliquer sur tes fonctions f1 à f6 et leurs derivées respectives que je re écris (car les images sont nulles trop petites on les voit mal)
bref ces fonctions avec celle-ci=\frac {2.\pi .(x-p_1)}{p})
que l'on retrouve sur la fonction notée f4 et sa derivée f'4
donc bref toutes ces fonctions qui se retrouvent dans la formule de f et de sa derivee f'
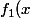 = \frac {1}{2}.cos(w_1.(x-p_1))+ \frac {1}{2})
= \frac {-w_1}{2}.sin(w_1.(x-p_1)))
 = \frac {-\lambda}{2}.cos(w_0.(x-p_1)+\pi)- \frac {\lambda}{2}+1)
= \frac {\lambda.w_0}{2}.sin(w_0.(x-p_1)+\pi))
 = q_1+q.sin(2^{-1}.\pi.p^{-1}.(x-p_1))+(2^{-1}.\pi^{-1}.q_1^{\prime}.p-4^{-1}.q).sin(2.\pi.p^{-1}.(x-p_1)))
= 2^{-1}.\pi.p^{-1}.q.cos(2^{-1}.\pi.p^{-1}.(x-p_1))+(q_1^{\prime}-2^{-1}.\pi.p^{-1}.q).cos(2.\pi.p^{-1}.(x-p_1)))
 = 2^{-1}.\pi^{-1}.p.(2^{-1}.\pi.p^{-1}.q+r). \frac {cos(v.h(x))-cos(w.h(x))}{w.sin(2.\pi.w)-v.sin(2.\pi.v)})
= (2^{-1}.\pi.p^{-1}.q+r) .\frac {w.sin(w.h(x))-v.sin(v.h(x))}{w.sin(2.\pi.w)-v.sin(2.\pi.v)})
 = \frac {1}{2^m}.(cos(w_0.(x-p_1))+1)^m)
= \frac {-m.w_0}{2^m}.sin(w_0.(x-p_1)).(cos(w_0.(x-p_1))+1)^{m-1})
 = \begin{pmatrix} 1-\frac {1}{2^{m_1}}.(cos(w_0.(x-p_1))+1)^{m_1} \end{pmatrix} .\begin{pmatrix} \frac {q}{p}.x-\frac {q.p_1}{p}+q_1+a.sin^l(w_2.(x-p_1))\end{pmatrix})
= \begin{pmatrix} 1-\frac {1}{2^{m_1}}.(cos(w_0.(x-p_1))+1)^{m_1} \end{pmatrix}.\begin{pmatrix} a.l.w_2.cos(w_2.(x-p_1)).sin^{l-1}(w_2.(x-p_1))+\frac {q}{p}\end{pmatrix} +...)
).(cos(w_0.(x-p_1))+1)^{m_1-1}. \begin{pmatrix}\frac {q}{p}.x-\frac{q.p_1}{p}+q_1+a.sin^l(w_2(x-p_1))\end{pmatrix})
alors l'ecriture de la fonction est la suivante
 = f_1(x).f_2(x).f_5(x).\begin{pmatrix} f_3(x)+f_4(x)-\frac {q}{p}.x+\frac {q.p_1}{p}-q_1\end{pmatrix} + f_5(x).\begin{pmatrix} \frac {q}{p}.x-\frac {q.p_1}{p}+q_1\end{pmatrix} +f_6(x))
= f_1(x).f_2(x).f_5^{\prime}(x).\begin{pmatrix} f_3(x)+f_4(x)-\frac {q}{p}.x+\frac {q.p_1}{p}-q_1\end{pmatrix} + f_5^{\prime}(x).\begin{pmatrix} \frac {q}{p}.x-\frac {q.p_1}{p}+q_1\end{pmatrix} +...)
.(f_1(x).f_2^{\prime}(x)+f_1^{\prime}(x).f_2(x)).\begin{pmatrix} f_3(x)+f_4(x)-\frac {q}{p}.x+\frac {q.p_1}{p}-q_1\end{pmatrix}+...)
.f_2(x).f_5(x). \begin{pmatrix} f_3^{\prime}(x)+f_4^{\prime}(x)-\frac {q}{p} \end{pmatrix} +\frac {q}{p}.f_5(x) +f_6^{\prime}(x))
juste avant que je tape ma fonction dans ma machine
ici j'explique tout en detail et j'ai re-écris ici les fonctions
je viens de voir que dans les images la fonction f4 et sa derivée f'4 était mal écrite une petite erreur d'écriture mais facilement reperable
bon bref tu as trois intervalles fermés [T0;T1],[T1;T2],[T2;T3]
tu t'occupe d'un intervalle puis de l'autre puis de l'autre
par exemple prenons le premier intervalle [T0;T1] , donc oublie les autres et comme apres c'est ce que tu va faire pour les autres intervalles (une fois que tu te sera occupé de celui là ) eh bien tu obtiendra une application de classe C1 (une seule fois derivable sur tout l'intervalle [T0;T3] et d'ailleurs son domaine de definition c'est
)
donc bref alors prenons le premier intervalle [T0;T1]
alors tu pose p1=T0 p2=T1 q1=g(T0) q2=g(T1) q'1=g'(T0) q'2=g'(T1)
g et g' sa derivée étant la fonction que tu recherche (mais que justement tu ne connais pas)
tu te donne tous les autres parametres tu est libre de te les choisir à ta guise comme tu veux
de toute façon tu obtiendra quand même f(p1)=q1,f(p2)=q2,f'(p1)=q'1,f'(p2)=q'2
dans la condition que tes autres parametres respectent ci-dessous :
mais attention choisi les de façon que tu obtienne l'inégalité
avec au choix tu choisi l'un des deux ci-dessous :
ou bien
puis determine
___________________________________
une fois que ça c'est fait alors tu pose
___________________________________
et là tu as tous les parametres pour les appliquer sur tes fonctions f1 à f6 et leurs derivées respectives que je re écris (car les images sont nulles trop petites on les voit mal)
bref ces fonctions avec celle-ci
donc bref toutes ces fonctions qui se retrouvent dans la formule de f et de sa derivee f'
alors l'ecriture de la fonction est la suivante
par alphamethyste » 16 Sep 2015, 03:58
bon j'ai commencé à taper les fonctions (c'est long je reprendrai soir-ce)
du coup je retourne dormir un peu
pour le reste : j'ai effacé les fonctions affichées sur le deuxième post(oui il y avait une erreur sur la f4(x) et sa derivée)
pour le reste aussi : au dernier post j'ai tout bien expliqué sur la manière de procéder et j'ai reécris ces fonctions (en plus l'image était de mauvaise qualité c'est tout juste s'il fallait pas une loupe pour les voir)
et enfin si il y a une autre erreur je le saurai quand j'aurai tapé ces fonctions sur ma machine
en fait c'est facile car je sais comment fonctionnent les fonctions f1(x) à f6(x) et la fonction f(x)
alors si jamais l'une d'elle fait pas ce que j'attend de elle ça sautera aux yeux laquelle et le pourquoi elle déconne
bon à plus
du coup je retourne dormir un peu
pour le reste : j'ai effacé les fonctions affichées sur le deuxième post(oui il y avait une erreur sur la f4(x) et sa derivée)
pour le reste aussi : au dernier post j'ai tout bien expliqué sur la manière de procéder et j'ai reécris ces fonctions (en plus l'image était de mauvaise qualité c'est tout juste s'il fallait pas une loupe pour les voir)
et enfin si il y a une autre erreur je le saurai quand j'aurai tapé ces fonctions sur ma machine
en fait c'est facile car je sais comment fonctionnent les fonctions f1(x) à f6(x) et la fonction f(x)
alors si jamais l'une d'elle fait pas ce que j'attend de elle ça sautera aux yeux laquelle et le pourquoi elle déconne
bon à plus
par alphamethyste » 16 Sep 2015, 12:34
bon c'est ok ça marche !!
il y avait une autre erreur sur la derivée de f6 mais j'ai re-edité
bon à présent j'ai oublié (expres) de parler du piège à éviter, exprès car chaque chose en son temps
quand on fait fonctionner ces fonctions et lorsque on prend les parametres suivants (ils sont autorisés mais il y a un piège à éviter)
les paramètres suivants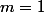
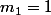ou 
ou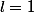
dans ce cas sur sa machine il faut re-taper les fonctions f5 et f6 avec leurs derivées à part
en ignorant les facteurs dans lesquels un exposant est zero et en ignorant les exposants de valeur 1
( par definition la machine est stupide elle va s'amuser à tout calculer des trucs du genre zero par quelque chose ou pire zero puissance zero et qu'elle te dise qu'elle ne sais pas calculer ça et du coup elle aura raison)
du coup pour m= 1 ne pas lui demander d'effectuer ça
mais plutôt lui demander d'effectuer ça = \frac {1}{2}.(cos(w_0.(x-p_1))+1))
toujours pour m=1 ne pas lui demander d'effectuer ça
mais plutôt lui demander d'effectuer ça
= \frac {-w_0}{2}.sin(w_0.(x-p_1)))
mais aussi pour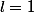 et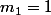
ne pas lui demander d'effectuer ça
mais plutôt lui demander d'effectuer ça
 = \begin{pmatrix} 1-\frac {1}{2 }.(cos(w_0.(x-p_1))+1) \end{pmatrix} .\begin{pmatrix} \frac {q}{p}.x-\frac {q.p_1}{p}+q_1+a.sin (w_2.(x-p_1))\end{pmatrix})
ne pas lui demander d'effectuer ça
Mais plutôt lui demander d'effectuer ça
= \begin{pmatrix} 1-\frac {1}{2 }.(cos(w_0.(x-p_1))+1) \end{pmatrix}.\begin{pmatrix} a.w_2.cos(w_2.(x-p_1)). +\frac {q}{p}\end{pmatrix} +...)
) . \begin{pmatrix}\frac {q}{p}.x-\frac{q.p_1}{p}+q_1+a.sin (w_2(x-p_1))\end{pmatrix})
il y avait une autre erreur sur la derivée de f6 mais j'ai re-edité
bon à présent j'ai oublié (expres) de parler du piège à éviter, exprès car chaque chose en son temps
quand on fait fonctionner ces fonctions et lorsque on prend les parametres suivants (ils sont autorisés mais il y a un piège à éviter)
les paramètres suivants
dans ce cas sur sa machine il faut re-taper les fonctions f5 et f6 avec leurs derivées à part
en ignorant les facteurs dans lesquels un exposant est zero et en ignorant les exposants de valeur 1
( par definition la machine est stupide elle va s'amuser à tout calculer des trucs du genre zero par quelque chose ou pire zero puissance zero et qu'elle te dise qu'elle ne sais pas calculer ça et du coup elle aura raison)
du coup pour m= 1 ne pas lui demander d'effectuer ça
mais plutôt lui demander d'effectuer ça
toujours pour m=1 ne pas lui demander d'effectuer ça
mais plutôt lui demander d'effectuer ça
mais aussi pour
ne pas lui demander d'effectuer ça
mais plutôt lui demander d'effectuer ça
ne pas lui demander d'effectuer ça
Mais plutôt lui demander d'effectuer ça
par alphamethyste » 16 Sep 2015, 21:59
j'ai modifié le message au lieu de poster un nouveau post et ça a effacé l'exemple ici mais son parametrage faisait que la fonction oscille trop
les valeur de m et m1 étaient trop petites par rapport à la grandeurs des derivées
les valeur de m et m1 étaient trop petites par rapport à la grandeurs des derivées
par alphamethyste » 17 Sep 2015, 02:43
autre exemple
pour la dérivée sur le point zero là j'ai pris une valeur de 10
car plus l'amplitude des valeurs des derivées sont importantes et plus la fonction oscille
et plus il faut augmenter les valeur de m et m1 pour réduire cette oscillation
et donc d'avoir une grande puissance de calcul (ce que ma machine n'a pas)
par ailleurs là j'ai changé d'echelle
sur l'axe des abscisses
100%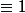
sur l'axe des ordonnées
=g(0\mu s)=0)
%,=10)
comme attendu
=14,367)
%,= 1,451451)
=29,049)
%,=1,479884)
=43,783)
%,=-3,297303)
ici on voit bien que la fonction oscille pas mal sur le segment de droite reliant le point (0;0) et le point (0.7;1) mais le pourcentage reste en deçà des 100% et au dessus de zero
=58,669)
%,=1,040719)
=71,906)
%,=1,377)
=85,795)
%,=1,405640)
=g(7\mu s)=100)
%,=0)
comme attendu
pour les autres intervalles on peut garder les mêmes parametres que ceux ci dessous
u=1
n=1
k=2
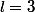
m=70 il faut une grande puissance de calcul pour éviter à la fonction d'osciller
m1=70 idem
m2=1
idem
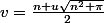
pour la dérivée sur le point zero là j'ai pris une valeur de 10
car plus l'amplitude des valeurs des derivées sont importantes et plus la fonction oscille
et plus il faut augmenter les valeur de m et m1 pour réduire cette oscillation
et donc d'avoir une grande puissance de calcul (ce que ma machine n'a pas)
par ailleurs là j'ai changé d'echelle
100%
pour les autres intervalles on peut garder les mêmes parametres que ceux ci dessous
u=1
n=1
k=2
m=70 il faut une grande puissance de calcul pour éviter à la fonction d'osciller
m1=70 idem
m2=1
par bartras » 19 Sep 2015, 17:35
J'ai réussi à obtenir quelque chose, bon le problème c'est que je ne sais pas sur quels paramètres jouer pour arriver à mes fins.
Mais surtout, je m'aperçois que c'est beaucoup trop lourd.
Ce que je cherchais à l'origine c'était d'avoir une formule simple avec mes quelques paramètres.
Là j'ai beaucoup beaucoup trop de formules à combiner, je ne pourrais pas le rentrer dans le modèle que je cherche à réaliser...
new excel : excelv2
Mais surtout, je m'aperçois que c'est beaucoup trop lourd.
Ce que je cherchais à l'origine c'était d'avoir une formule simple avec mes quelques paramètres.
Là j'ai beaucoup beaucoup trop de formules à combiner, je ne pourrais pas le rentrer dans le modèle que je cherche à réaliser...
new excel : excelv2
par alphamethyste » 19 Sep 2015, 18:01
bon apres il y aurai bien deux autres solutions...
la premiere (et bon à la limite la plus simple aussi )serai d'abandonner cette fonction et d'essayer d'exprimer ta fonction par une simple equation polynomiale c'est pas compliqué (localement ta fonction a un peu l'air d'avoir la forme d'une fonction de degre 3
J'ai dit localement c'est à dire en T1 la derivée est nulle puis en T3 la derivée est de nouveau nulle
donc sa derivée est d'ordre deux
sinon de ce que tu as vu pour la premiere intervalle cela te conviens t-il ?
évidemment ces calculs là je les ai fait sur une machine programmable TI
si tu prend les mêmes parametres que j'ai ecris ici tu obtiens la même chose
(c'est obligé à moins que les calculs de la machine soient faussés par des erreurs d'arrondis en appliquant des exponentielles (ici par exemple m=70 sert d'exposant, car il faut que l'exposant soit d'autant plus grand que tes derivées aux bornes sont importantes en valeur absolues et augmente les oscillations de ta fonction entre les deux points (Ti,f(Ti)) et (Ti+1,f(Ti+1))
bon apres c'est lourd (tu as vu il a fallu que je pose m=70 pour qu'une derivée au borne de valeur 10 ne fasse pas trop osciller la fonction )
donc tu vois c'est lourd comme calcul et il vaut mieux que la machine travaille avec au mois 15 chiffres significatifs si cette fonction t'interesse toujours
bon apres il y aurai bien une derniere solution...(mais encore là sous condition que l'importance en valeur absolue de tes derivees aux bornes soit maitrisé par un exposant m tres grand)
tu augmente la quantité d'intervalle de sorte que (à condition que tes derivées aux bornes ne soit pas trop importantes en valeurs absolues car sinon m doit devenir tres grand pour attenuer les oscillations et donc du coup tu dois pouvoir disposer d'une grande capacite de calcul afin que des erreurs d'arrondis de la machine ne viennent interferer sur le resultat
la premiere (et bon à la limite la plus simple aussi )serai d'abandonner cette fonction et d'essayer d'exprimer ta fonction par une simple equation polynomiale c'est pas compliqué (localement ta fonction a un peu l'air d'avoir la forme d'une fonction de degre 3
J'ai dit localement c'est à dire en T1 la derivée est nulle puis en T3 la derivée est de nouveau nulle
donc sa derivée est d'ordre deux
sinon de ce que tu as vu pour la premiere intervalle cela te conviens t-il ?
évidemment ces calculs là je les ai fait sur une machine programmable TI
si tu prend les mêmes parametres que j'ai ecris ici tu obtiens la même chose
(c'est obligé à moins que les calculs de la machine soient faussés par des erreurs d'arrondis en appliquant des exponentielles (ici par exemple m=70 sert d'exposant, car il faut que l'exposant soit d'autant plus grand que tes derivées aux bornes sont importantes en valeur absolues et augmente les oscillations de ta fonction entre les deux points (Ti,f(Ti)) et (Ti+1,f(Ti+1))
bon apres c'est lourd (tu as vu il a fallu que je pose m=70 pour qu'une derivée au borne de valeur 10 ne fasse pas trop osciller la fonction )
donc tu vois c'est lourd comme calcul et il vaut mieux que la machine travaille avec au mois 15 chiffres significatifs si cette fonction t'interesse toujours
bon apres il y aurai bien une derniere solution...(mais encore là sous condition que l'importance en valeur absolue de tes derivees aux bornes soit maitrisé par un exposant m tres grand)
tu augmente la quantité d'intervalle de sorte que (à condition que tes derivées aux bornes ne soit pas trop importantes en valeurs absolues car sinon m doit devenir tres grand pour attenuer les oscillations et donc du coup tu dois pouvoir disposer d'une grande capacite de calcul afin que des erreurs d'arrondis de la machine ne viennent interferer sur le resultat
par bartras » 19 Sep 2015, 18:19
Oui le dernier fichier fonctionne, le problème reste la longueur des équations..
Je suis reparti sur la formule du début :
f(t) = k * ( exp(-A*t) - exp(-B*t) )
Elle me plait bien, mais il faut arriver à faire une approximation.
J'ai posé :
f(0) = 0
f(t1) = k
f(t2) = k/2
sachant :
k = Vp*(1+tVp)
t1 = 40*(1+tT1)
t2 = 120*(1+tT2)
et mes données d'entrées sont :
Vp ; tVp ; tT1 ; tT2
mes inconnues :
A ; B
Est ce qu'il n'est pas possible d'approximer cette fonction pour déterminer une expression de A et B pas trop longue à partir de mes données ?
Je suis reparti sur la formule du début :
f(t) = k * ( exp(-A*t) - exp(-B*t) )
Elle me plait bien, mais il faut arriver à faire une approximation.
J'ai posé :
f(0) = 0
f(t1) = k
f(t2) = k/2
sachant :
k = Vp*(1+tVp)
t1 = 40*(1+tT1)
t2 = 120*(1+tT2)
et mes données d'entrées sont :
Vp ; tVp ; tT1 ; tT2
mes inconnues :
A ; B
Est ce qu'il n'est pas possible d'approximer cette fonction pour déterminer une expression de A et B pas trop longue à partir de mes données ?
par alphamethyste » 19 Sep 2015, 18:35
Matheux philosophe a écrit:Et si vous cherchiez plutôt à déterminer et à calculer un polynôme d'interpolation suivant une des méthodes existantes, vraisemblablement de degré 3 ou plus :
Par exemple un polynôme de Lagrange ou un autre type de polynôme.
c'est ce que je lui ai proposé tout à l'heure (apres tout si les valeurs des derivées sur les points donnés en entrés n'ont pas d'importance à la limite c'est le mieux )
sinon avec ma fonction on est toujours sûr que quelque soit les données dont on dispose et de la valeur des derivées que l'on pose sur ces données on aura toujours le resultat recherché sans avoir à faire d'approximation
exemple sur le premier intervalle ->(mais pour une derivée de 10 j'ai du prendre un exposant de 70 , plus la valeur absolue des derivées aux bornes sont importantes plus il est necessaire de disposer d'une machine travaillant sur un nombre important de chiffres significatifs -là dans l'exemple ci-dessous 15 chiffres sont necessaires pour avoir ça )
je pense que c'est bien ce qu'il recherchai (s'eviter de faire des approximations non ?
alphamethyste a écrit:autre exemple
par bartras » 19 Sep 2015, 19:05
J'ai fais avec Lagrange en prenant ça :
x0 = 0 & y0 = 0
x1 = 40 & y1 = 1
x2 = 120 & y2 = 0.5
x3 = 500 & y3 = 0.001
Et je trouve la formule :
P(X) = 5.42E-7 * X^3 - 4.95E-4 * X^2 + 3.8E-2 * X
Mais ça n'a pas l'air juste quand j'affiche en courbe...
Quels coefficient trouvez vous ?
x0 = 0 & y0 = 0
x1 = 40 & y1 = 1
x2 = 120 & y2 = 0.5
x3 = 500 & y3 = 0.001
Et je trouve la formule :
P(X) = 5.42E-7 * X^3 - 4.95E-4 * X^2 + 3.8E-2 * X
Mais ça n'a pas l'air juste quand j'affiche en courbe...
Quels coefficient trouvez vous ?
par bartras » 19 Sep 2015, 19:09
Matheux philosophe a écrit:Tu m'as l'air pourtant bien calé, dans cette discussion, et ton niveau ne semble pas ou ne semble plus refléter celui que tu prétends avoir :
L'exercice que te propose bartras est soit d'un niveau d'une bonne TS, soit du niveau d'une L1 voire plus.
Moi, j'ai un M2 R, et ce problème ne me semble pas aussi limpide qu'il te paraît.
En étant rigoureux on y arrive avec sa première méthode, mais c'est en effet très lourd et pas très limpide...
Mon besoin n'est pas la précision exacte mais vraiment réussir à m'approcher de mes valeurs avec une formule plutôt simple car il s'agit de la rentrer dans un logiciel de simu élec' et donc qui ne permet pas de faire des calculs mastodon ^^
par bartras » 19 Sep 2015, 20:59
Est ce que quelqu'un saurait approximer, interpoler ce système de 3 inconnues :
1 = k * ( exp(-A*5.52e-6) - exp(-B*5.52e-6) )
0.5 = k * ( exp(-A*82.8e-6) - exp(-B*82.8e-6) )
0 = B * k * exp(-B*5.52e-6) - A * k * exp(-A*5.52e-6)
???
1 = k * ( exp(-A*5.52e-6) - exp(-B*5.52e-6) )
0.5 = k * ( exp(-A*82.8e-6) - exp(-B*82.8e-6) )
0 = B * k * exp(-B*5.52e-6) - A * k * exp(-A*5.52e-6)
???
par alphamethyste » 19 Sep 2015, 21:14
bartras a écrit:
1 = k * ( exp(-A*5.52e-6) - exp(-B*5.52e-6) )
0.5 = k * ( exp(-A*82.8e-6) - exp(-B*82.8e-6) )
0 = B * k * exp(-B*5.52e-6) - A * k * exp(-A*5.52e-6)
une methode numerique (rapide : quadratique )est possible mais décante un peu ton systeme
il est aussi tres bon d'exprimer des trucs du genre 5.52 e-6 par 0.00000552 car le "e"
on sait des fois pas trop ce qu'il veut dire (si des fois tu veux dire la base du log neperien même si je suppose que exp est une exponentielle de base e neperienne)
decante un peu ça et exprime tes parametres sous forme de fractions
0,00000552= 552/ 100000000 et ça se simplifie
puis exprime le k de ta première equation par les deux autres inconnues A et B
puis exprime A par l'inconnue B de la deuxieme
il te restera une equation d'inconnue A et bon une methode numerique quadratique (donc rapide est possible ) que je te donnerai cette nuit si je dort pas ou alors demain ...
bref pour un truc rapide qui converge rapidement
par bartras » 20 Sep 2015, 13:28
j'obtiens
k = 1 / ( exp(-A*t1) - exp(-B*t1) )
A = -1/t2 * ln [ ( 0.5 + k * exp(-B*t2) ) / k ]
avec t1 = 552 / 100000000 et t2 = 828/10000000
k = 1 / ( exp(-A*t1) - exp(-B*t1) )
A = -1/t2 * ln [ ( 0.5 + k * exp(-B*t2) ) / k ]
avec t1 = 552 / 100000000 et t2 = 828/10000000
37 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 13 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :