Sens variation suite

[capitaine nuggets]

C'est quoi la question exactement dans ton exo ? "Prouver le sens de variation de la fonction" n'a pas vraiment de sens...

Si personne d'autres ne propose une méthode pour 1S, j'essaierais de voir ça plus en détail ce soir si j'ai le temps. Pour l'instant, je ne vois pas trop comment faire ton exo.

[marco_seb]

en fait je viens de le résoudre en calculant les 1ers termes.
C'est une suite ni croissante, ni décroissante donc une suite alternée!

[capitaine nuggets]

Ca ne veut rien dire : il se peut très bien qu'à partir d'un certain rang ta suite soit monotone.

Exemple : la suite définie par , puis paf ! 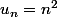pour .

[capitaine nuggets]

Re-salut !

J'ai essayé une autre méthode : on peut montrer que .
Considère la fonction définie sur 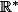par .
est décroissante donc si donc , et ainsi , on a , ou encore quel que soit n, .

Donc, si la question est bien de chercher les variations de la suite , elle n'est ni croissante, ni décroissante, puisqu'elle croit puis décroit après chaque indice suivant.

Après une étude un peu plus approfondie, on a mieux : on peut considérer deux suites et respectivement définies par et , et de montrer que l'une est strictement croissante et l'autre strictement décroissante et qu'elle convergent vers la même limite.

Remarque : Ca me fait penser, mais même en 1S, on ne voit pas le raisonnement par récurrence ?

[capitaine nuggets]

Re-salut !

J'ai essayé une autre méthode : on peut montrer que .
Considère la fonction définie sur 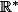par .
est décroissante donc si donc , et ainsi , on a , ou encore quel que soit n, .

Donc, si la question est bien de chercher les variations de la suite , elle n'est ni croissante, ni décroissante, puisqu'elle croit puis décroit après chaque indice suivant.

Après une étude un peu plus approfondie, on a mieux : on peut considérer deux suites et respectivement définies par et , et de montrer que l'une est strictement croissante et l'autre strictement décroissante et qu'elle convergent vers la même limite (on dit que ces deux suites sont adjacentes, mais je suppose que tu n'as pas vu cette notion...).

Remarque : Ca me fait penser, mais même en 1S, on ne voit pas le raisonnement par récurrence ?

[zygomatique]

pour compléter la réponse plus simplement du capitaine ::

1/ w_n est positif

2/

donc w(n + 2) et w(n + 1) sont dans l'ordre inverse de w(n + 1) et w(n)

....

:lol3:

[marco_seb]

N'insistez pas messieurs,
Cette suite est ni croissante, ni décroissante!!
C'est une suite alternée!!

[zygomatique]

ben c'est ce que je te prouve au dessus ....