Sens de variation d'une suite - calcul d'une somme - suite
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 05 Nov 2009, 01:11
par Dinozzo13 » 05 Nov 2009, 01:11
Bonjour, j'ai étudier le sens de variation de la suite
_{n\ge1})
définie par
^n}{n^2})
, pourriez-vous me dire si le raisonement est bon, merci d'avance.
Pour tout
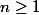
, je calcule

:
^{n+1}}{(n+1)^2})
.
Ensuite, je suis censé choisir méthodiquement entre calculer
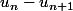
et
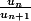
.
Mais je vois rapidement qu'on va pédaler dans la semoule ^^.
J'ai donc dit que
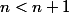
, or
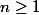
donc
^2)
; puis que
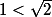
donc
^n<(\sqrt 2)^{n+1})
.
Par conséquent,
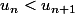
donc
)
est strictement croissante.
Ai-je bon ?
-
zerkel
- Membre Relatif
- Messages: 134
- Enregistré le: 01 Nov 2009, 18:08
-
 par zerkel » 05 Nov 2009, 01:34
par zerkel » 05 Nov 2009, 01:34
bonsoir,
désolée mais ton raisonnement a une erreur pour t'en convaincre calcule
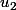
et
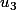
.
-
zerkel
- Membre Relatif
- Messages: 134
- Enregistré le: 01 Nov 2009, 18:08
-
 par zerkel » 05 Nov 2009, 02:05
par zerkel » 05 Nov 2009, 02:05
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 05 Nov 2009, 02:36
par Dinozzo13 » 05 Nov 2009, 02:36
Je trouve :
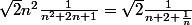
Mais après je ne vois pas :triste: .
-
zerkel
- Membre Relatif
- Messages: 134
- Enregistré le: 01 Nov 2009, 18:08
-
 par zerkel » 05 Nov 2009, 02:53
par zerkel » 05 Nov 2009, 02:53
Attention erreur tu as simplifié par

en haut et par n en bas!
tu veux par exemple chercher quand cela est plus grand que 1.
Donc tu arrives à l'inéquation
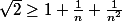
Tu poses alors
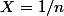
et tu étudies le signe d'un polynôme du second degré.
Pour la suite on verra plus tard si tu ne trouves pas tout seul

-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 05 Nov 2009, 03:04
par Dinozzo13 » 05 Nov 2009, 03:04
je vois pas comment tu fais pour aller de
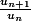
à
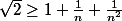

.
Tu pourrais me détailler tout ça si cela ne te gêne pas :doh: .
-
zerkel
- Membre Relatif
- Messages: 134
- Enregistré le: 01 Nov 2009, 18:08
-
 par zerkel » 05 Nov 2009, 03:19
par zerkel » 05 Nov 2009, 03:19
En fait tu veux comparer
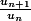
avec 1.
Par exemple tu étudies
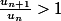
.
Tu as
^2} \times \frac{n^2}{sqrt{2}^{n}}=\frac{n^2 sqrt{2}}{(n+1)^2}=\frac{n^2sqrt{2}}{n^2(\frac{1}{n}+1)^2}= \frac{sqrt{2}}{(\frac{1}{n}+1)^2})
Donc ce que tu veux par exemple c'est savoir quand
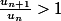
.
C'est-à-dire
^2} >1)
Cela te donne
^2)
.
Donc là tu fais
^2-\sqrt{2}>0)
Et tu poses X=

.
Pour étudier quand cela est positif.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 05 Nov 2009, 03:26
par Dinozzo13 » 05 Nov 2009, 03:26
-
zerkel
- Membre Relatif
- Messages: 134
- Enregistré le: 01 Nov 2009, 18:08
-
 par zerkel » 05 Nov 2009, 03:27
par zerkel » 05 Nov 2009, 03:27
Ouais voilà ensuite tu trouves du coup le signe de ton expression et tu remplaces X par sa valeur.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 05 Nov 2009, 03:33
par Dinozzo13 » 05 Nov 2009, 03:33
Donc
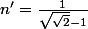
et
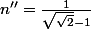
-
zerkel
- Membre Relatif
- Messages: 134
- Enregistré le: 01 Nov 2009, 18:08
-
 par zerkel » 05 Nov 2009, 03:34
par zerkel » 05 Nov 2009, 03:34
ouais c'est pour ses valeurs là que les changements se font
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 05 Nov 2009, 03:40
par Dinozzo13 » 05 Nov 2009, 03:40
Dinozzo13 a écrit:Donc
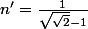
et
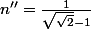
Donc ce quotient est strictement positif ssi
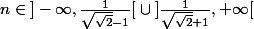
?
-
zerkel
- Membre Relatif
- Messages: 134
- Enregistré le: 01 Nov 2009, 18:08
-
 par zerkel » 05 Nov 2009, 03:42
par zerkel » 05 Nov 2009, 03:42
oui, enfin bon pour les nombres négatifs on s'en fiche et tu dois calculer une approximation de
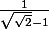
puisqu'on est quand même en train de regarder les termes de la suites à partir desquels ça va être croissant.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 05 Nov 2009, 03:44
par Dinozzo13 » 05 Nov 2009, 03:44
zerkel a écrit:oui, enfin bon pour les nombres négatifs on s'en fiche et tu dois calculer une approximation de
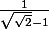
puisqu'on est quand même en train de regarder les termes de la suites à partir desquels ça va être croissant.
Je trouve
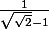
>5
-
zerkel
- Membre Relatif
- Messages: 134
- Enregistré le: 01 Nov 2009, 18:08
-
 par zerkel » 05 Nov 2009, 03:45
par zerkel » 05 Nov 2009, 03:45
normal, donc maintenant tu es à deux doigts de la conclusion
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 05 Nov 2009, 03:54
par Dinozzo13 » 05 Nov 2009, 03:54
ah oui, si
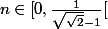
alors
)
est strictement décroissante.
si
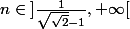
alors
)
est strictement croissante.
-
zerkel
- Membre Relatif
- Messages: 134
- Enregistré le: 01 Nov 2009, 18:08
-
 par zerkel » 05 Nov 2009, 03:55
par zerkel » 05 Nov 2009, 03:55
tu n'aimes pas les entiers toi lol
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 05 Nov 2009, 03:57
par Dinozzo13 » 05 Nov 2009, 03:57
J'ai voulu être le plus précis possible, je pense que la rigueur est importante :zen: .
Dites moi, il y a un autre exercice, qui selon moi est plus dur, où je dois démontrer un somme assez moche :ptdr: , accepteriez-vous de m'aider ? :cry:
-
zerkel
- Membre Relatif
- Messages: 134
- Enregistré le: 01 Nov 2009, 18:08
-
 par zerkel » 05 Nov 2009, 03:59
par zerkel » 05 Nov 2009, 03:59
tu peux me tutoyer, je ne suis pas si vieille que ça quand même :p
Oui oui il me reste encore un bon nombre de pages avant de finir mon chapitre et d'aller dormir, donc je suis ok pour t'aider.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 05 Nov 2009, 04:04
par Dinozzo13 » 05 Nov 2009, 04:04
zerkel a écrit:tu peux me tutoyer, je ne suis pas si vieille que ça quand même :p
:we: ouais remarque pour 5 ans de différence.
C'est juste que certaines personnes n'aiment pas être tutoyées.
zerkel a écrit:Oui oui il me reste encore un bon nombre de pages avant de finir mon chapitre et d'aller dormir, donc je suis ok pour t'aider.
Merci, ça faisait un an que je bloquais dessus :ptdr: , alors, on me dit que
)
est une suite arithmétique dont tous les termes sont strictement positifs. On me demande de prouver que :
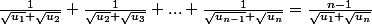
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 86 invités