Sens de variation d'une suite - calcul d'une somme - suite
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 05 Nov 2009, 04:50
par Dinozzo13 » 05 Nov 2009, 04:50
Et si on posait
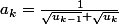
équivaut à
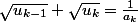
et que l'on remplace dans la somme ?
-
zerkel
- Membre Relatif
- Messages: 134
- Enregistré le: 01 Nov 2009, 18:08
-
 par zerkel » 05 Nov 2009, 04:51
par zerkel » 05 Nov 2009, 04:51
pourquoi pas, je te laisse tenter
-
zerkel
- Membre Relatif
- Messages: 134
- Enregistré le: 01 Nov 2009, 18:08
-
 par zerkel » 05 Nov 2009, 04:59
par zerkel » 05 Nov 2009, 04:59
bon ça y est, j'y suis c'est bien une récurrence :p
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 05 Nov 2009, 04:59
par Dinozzo13 » 05 Nov 2009, 04:59
OK, bon je me lance alors ^^ ?
-
zerkel
- Membre Relatif
- Messages: 134
- Enregistré le: 01 Nov 2009, 18:08
-
 par zerkel » 05 Nov 2009, 05:05
par zerkel » 05 Nov 2009, 05:05
Bon pour le moment je pose
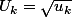
Je te laisse l'initialisation la flemme de taper...
On suppose que l'on a
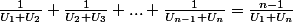
Je vais montrer que
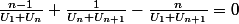
-
zerkel
- Membre Relatif
- Messages: 134
- Enregistré le: 01 Nov 2009, 18:08
-
 par zerkel » 05 Nov 2009, 05:08
par zerkel » 05 Nov 2009, 05:08
On met tout au même dénominateur, et en fait on arrête d'écrire le dénominateur parce qu'on va montrer que le numérateur est nul.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 05 Nov 2009, 05:09
par Dinozzo13 » 05 Nov 2009, 05:09
Au fait, cette suite est définie pour tout
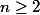
.
-
zerkel
- Membre Relatif
- Messages: 134
- Enregistré le: 01 Nov 2009, 18:08
-
 par zerkel » 05 Nov 2009, 05:18
par zerkel » 05 Nov 2009, 05:18
On développe tout ça et on fait une première simplification des termes égaux, il nous reste:
U_{n+1}^2+U_{1}^2-nU_{n}^2)
On peut revenir à la notation
u_{n+1}^2+u_{1}^2-nu_{n}^2)
Et là on se sert du fait qu'elle est arithmétique et roulement de tambour on tombe sur 0.
-
zerkel
- Membre Relatif
- Messages: 134
- Enregistré le: 01 Nov 2009, 18:08
-
 par zerkel » 05 Nov 2009, 05:20
par zerkel » 05 Nov 2009, 05:20
Bon je t'ai beaucoup spoilé pour la récurrence mais bon comme ça au moins tu as toutes les étapes si jamais tu bloques.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 05 Nov 2009, 05:21
par Dinozzo13 » 05 Nov 2009, 05:21
Je pose
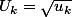
Si

alors
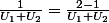
, l'égalité est vérifiée.
Supposons que
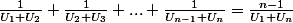
, montrons qu'alors
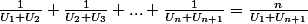
.
D'après l'hypotèse de récurrence :
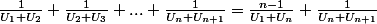
.
Mais après je vois pas

-
zerkel
- Membre Relatif
- Messages: 134
- Enregistré le: 01 Nov 2009, 18:08
-
 par zerkel » 05 Nov 2009, 05:23
par zerkel » 05 Nov 2009, 05:23
cf post # 45
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 05 Nov 2009, 05:24
par Dinozzo13 » 05 Nov 2009, 05:24
zerkel a écrit:Je vais montrer que
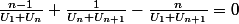
Pourquoi montrer ça ?
-
zerkel
- Membre Relatif
- Messages: 134
- Enregistré le: 01 Nov 2009, 18:08
-
 par zerkel » 05 Nov 2009, 05:26
par zerkel » 05 Nov 2009, 05:26
parce que c'est plus facile de prouver qu'un "truc" vaut zéro plutôt que de montrer qu'un "bidule" égale un "machin"!
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 05 Nov 2009, 05:27
par Dinozzo13 » 05 Nov 2009, 05:27
ok, c'est bon, et une fois ça démontrer, ça y est on a justifié l'égalité ?
-
zerkel
- Membre Relatif
- Messages: 134
- Enregistré le: 01 Nov 2009, 18:08
-
 par zerkel » 05 Nov 2009, 05:38
par zerkel » 05 Nov 2009, 05:38
Oui parce que pour montrer ça on a juste "fait passer" le terme de droite à gauche et on a montré l'égalité par la suite.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 05 Nov 2009, 05:42
par Dinozzo13 » 05 Nov 2009, 05:42
Donc l'exo est fini ^^.
Si ça te gêne pas j'en aurai peut-être un autre cet aprem' tu seras là ou non pour m'aider ?
-
zerkel
- Membre Relatif
- Messages: 134
- Enregistré le: 01 Nov 2009, 18:08
-
 par zerkel » 05 Nov 2009, 05:43
par zerkel » 05 Nov 2009, 05:43
Normalement je serai là, par contre je ne me lèverai probablement pas avant 13h30-14h, faut bien que je dorme aussi :p
Bonne nuit si t'y vas.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 05 Nov 2009, 05:48
par Dinozzo13 » 05 Nov 2009, 05:48
oh t'inquiète pas pour ça, moi aussi je suis mort, ça doit faire 23h que je suis levé, bonne nuit ^^ :we:
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 05 Nov 2009, 14:22
par Dinozzo13 » 05 Nov 2009, 14:22
Salut !
Voci donc un autre exo ou je bute, je ne suis pas là pour le moment donc je te laisse y réfléchir ^^.
1.
)
est une suite telle que, pout tout entier n non nul :
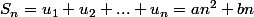
(

et

sont des réels).
Quelle est la nature de la suite
)
?
2. Si
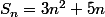
, calculer
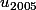
.
Je reviendrai ce soir pour que tu m'aide, merci encore ^^.

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 05 Nov 2009, 14:31
par Ericovitchi » 05 Nov 2009, 14:31
Tu écris
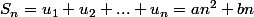
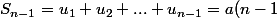^2+b(n-1))
Tu fais
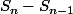
à gauche tu trouves

, tu simplifies à droite, et la nature de la suite

va t'apparaître simplement.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 71 invités
