Hello à tous,
En maths aujourd'hui, nous avons vu ce que signifiait la partition d'un ensemble.
Suite à quoi je me suis posé la légitime question : si j'ai un ensemble fini à, disons, n éléments, est-ce que je peux déterminer le nombre de partitions de cet ensemble ? Il est nécessairement fini, mais je n'arrive pas à l'expliciter ...
En fait je n'ai aucune idée de la difficulté de la question :ptdr:
Voila est-ce que quelqu'un pourrait m'aider ?
Lucas
PS : J'ai posté dans la section supérieur, pas par prétention, mais cela me semble la section la plus adaptée. :lol3:
Nombre de partitions
7 messages
- Page 1 sur 1
Salut,
C'est une très bonne question et ce n'est pas évident du tout a calculer.
Mais avant toute chose, il faut s'entendre très précisément sur ce que l'on appelle une "partition" et, surtout sur ce que l'on va appeler des "partitions différentes".
Par exemple, si on veut qu'il n'y ait qu'un nombre fini de partitions (d'un ensemble fini), il faut évidement exclure le fait de prendre l'ensemble vide parmi les éléments de la partitions(ou alors, accepter de le prendre, mais pas plus d'une fois).
Après, concernant les partitions différentes, il faut s'entendre pour savoir si on regarde une partition comme un ensemble (d'ensembles) donc dans lequel il n'y a pas de notion d'ordre des éléments ou bien si une partition est un n-uplet (d'ensembles) dans laquelle il y a une notion d'ordre des éléments.
Pour te donner un exemple, si X={a,b,c}, est- ce qu'on considère que la partition formée de {1} et {2,3} est la même que celle formée de {2,3} et {1} ?
On a bien {{1},{2,3}}={{2,3},{1}} mais par contre ({1},{2,3})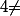 ({2,3},{1})
({2,3},{1})
En général, dans le contexte où on veut compter le nombre de partitions, on considère qu'une partition est un ensemble d'ensembles (pouvant contenir l'ensemble vide) mais dans d'autres contextes, ça peut être l'autre solution la plus adaptée.
C'est une très bonne question et ce n'est pas évident du tout a calculer.
Mais avant toute chose, il faut s'entendre très précisément sur ce que l'on appelle une "partition" et, surtout sur ce que l'on va appeler des "partitions différentes".
Par exemple, si on veut qu'il n'y ait qu'un nombre fini de partitions (d'un ensemble fini), il faut évidement exclure le fait de prendre l'ensemble vide parmi les éléments de la partitions(ou alors, accepter de le prendre, mais pas plus d'une fois).
Après, concernant les partitions différentes, il faut s'entendre pour savoir si on regarde une partition comme un ensemble (d'ensembles) donc dans lequel il n'y a pas de notion d'ordre des éléments ou bien si une partition est un n-uplet (d'ensembles) dans laquelle il y a une notion d'ordre des éléments.
Pour te donner un exemple, si X={a,b,c}, est- ce qu'on considère que la partition formée de {1} et {2,3} est la même que celle formée de {2,3} et {1} ?
On a bien {{1},{2,3}}={{2,3},{1}} mais par contre ({1},{2,3})
En général, dans le contexte où on veut compter le nombre de partitions, on considère qu'une partition est un ensemble d'ensembles (pouvant contenir l'ensemble vide) mais dans d'autres contextes, ça peut être l'autre solution la plus adaptée.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Salut,
C'est une très bonne question et ce n'est pas évident du tout a calculer.
Mais avant toute chose, il faut s'entendre très précisément sur ce que l'on appelle une "partition" et, surtout sur ce que l'on va appeler des "partitions différentes".
Par exemple, si on veut qu'il n'y ait qu'un nombre fini de partitions (d'un ensemble fini), il faut évidement exclure le fait de prendre l'ensemble vide parmi les éléments de la partitions(ou alors, accepter de le prendre, mais pas plus d'une fois).
Après, concernant les partitions différentes, il faut s'entendre pour savoir si on regarde une partition comme un ensemble (d'ensembles) donc dans lequel il n'y a pas de notion d'ordre des éléments ou bien si une partition est un n-uplet (d'ensembles) dans laquelle il y a une notion d'ordre des éléments.
Pour te donner un exemple, si X={a,b,c}, est- ce qu'on considère que la partition formée de {1} et {2,3} est la même que celle formée de {2,3} et {1} ?
On a bien {{1},{2,3}}={{2,3},{1}} mais par contre ({1},{2,3})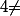 ({2,3},{1})
({2,3},{1})
En général, dans le contexte où on veut compter le nombre de partitions, on considère qu'une partition est un ensemble d'ensembles (pouvant contenir l'ensemble vide) mais dans d'autres contextes, ça peut être l'autre solution la plus adaptée.
C'est une très bonne question et ce n'est pas évident du tout a calculer.
Mais avant toute chose, il faut s'entendre très précisément sur ce que l'on appelle une "partition" et, surtout sur ce que l'on va appeler des "partitions différentes".
Par exemple, si on veut qu'il n'y ait qu'un nombre fini de partitions (d'un ensemble fini), il faut évidement exclure le fait de prendre l'ensemble vide parmi les éléments de la partitions(ou alors, accepter de le prendre, mais pas plus d'une fois).
Après, concernant les partitions différentes, il faut s'entendre pour savoir si on regarde une partition comme un ensemble (d'ensembles) donc dans lequel il n'y a pas de notion d'ordre des éléments ou bien si une partition est un n-uplet (d'ensembles) dans laquelle il y a une notion d'ordre des éléments.
Pour te donner un exemple, si X={a,b,c}, est- ce qu'on considère que la partition formée de {1} et {2,3} est la même que celle formée de {2,3} et {1} ?
On a bien {{1},{2,3}}={{2,3},{1}} mais par contre ({1},{2,3})
En général, dans le contexte où on veut compter le nombre de partitions, on considère qu'une partition est un ensemble d'ensembles (pouvant contenir l'ensemble vide) mais dans d'autres contextes, ça peut être l'autre solution la plus adaptée.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Salut,
C'est une très bonne question et ce n'est pas évident du tout a calculer.
Mais avant toute chose, il faut s'entendre très précisément sur ce que l'on appelle une "partition" et, surtout sur ce que l'on va appeler des "partitions différentes".
Par exemple, si on veut qu'il n'y ait qu'un nombre fini de partitions (d'un ensemble fini), il faut évidement exclure le fait de prendre l'ensemble vide parmi les éléments de la partitions(ou alors, accepter de le prendre, mais pas plus d'une fois).
Après, concernant les partitions différentes, il faut s'entendre pour savoir si on regarde une partition comme un ensemble (d'ensembles) donc dans lequel il n'y a pas de notion d'ordre des éléments ou bien si une partition est un n-uplet (d'ensembles) dans laquelle il y a une notion d'ordre des éléments.
Pour te donner un exemple, si X={a,b,c}, est- ce qu'on considère que la partition formée de {1} et {2,3} est la même que celle formée de {2,3} et {1} ?
On a bien {{1},{2,3}}={{2,3},{1}} mais par contre ({1},{2,3})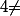 ({2,3},{1})
({2,3},{1})
En général, dans le contexte où on veut compter le nombre de partitions, on considère qu'une partition est un ensemble d'ensembles (non vides) mais dans d'autres contextes, ça peut être l'autre solution la plus adaptée.
C'est une très bonne question et ce n'est pas évident du tout a calculer.
Mais avant toute chose, il faut s'entendre très précisément sur ce que l'on appelle une "partition" et, surtout sur ce que l'on va appeler des "partitions différentes".
Par exemple, si on veut qu'il n'y ait qu'un nombre fini de partitions (d'un ensemble fini), il faut évidement exclure le fait de prendre l'ensemble vide parmi les éléments de la partitions(ou alors, accepter de le prendre, mais pas plus d'une fois).
Après, concernant les partitions différentes, il faut s'entendre pour savoir si on regarde une partition comme un ensemble (d'ensembles) donc dans lequel il n'y a pas de notion d'ordre des éléments ou bien si une partition est un n-uplet (d'ensembles) dans laquelle il y a une notion d'ordre des éléments.
Pour te donner un exemple, si X={a,b,c}, est- ce qu'on considère que la partition formée de {1} et {2,3} est la même que celle formée de {2,3} et {1} ?
On a bien {{1},{2,3}}={{2,3},{1}} mais par contre ({1},{2,3})
En général, dans le contexte où on veut compter le nombre de partitions, on considère qu'une partition est un ensemble d'ensembles (non vides) mais dans d'autres contextes, ça peut être l'autre solution la plus adaptée.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Darkwolftech a écrit:Hello à tous,
En maths aujourd'hui, nous avons vu ce que signifiait la partition d'un ensemble.
Suite à quoi je me suis posé la légitime question : si j'ai un ensemble fini à, disons, n éléments, est-ce que je peux déterminer le nombre de partitions de cet ensemble ? Il est nécessairement fini, mais je n'arrive pas à l'expliciter ...
En fait je n'ai aucune idée de la difficulté de la question :ptdr:
Voila est-ce que quelqu'un pourrait m'aider ?
Lucas
PS : J'ai posté dans la section supérieur, pas par prétention, mais cela me semble la section la plus adaptée. :lol3:
Très bonne question!
Si tu considères que les éléments sont distincts, ce sont les nombres de Bell.
Essaie de calculer B(n+1) en fonction des précédents!
Il y a un raisonnement combinatoire qui donne la formule.
Luc
Ben314 a écrit:En général, dans le contexte où on veut compter le nombre de partitions, on considère qu'une partition est un ensemble d'ensembles (non vides) mais dans d'autres contextes, ça peut être l'autre solution la plus adaptée.
Ok j'avais effectivement pensé à ce petit problème ... donc pour toi on ne prend pas en compte l'ordre des ensembles ! C'est plus cool ça ... :ptdr:
Après pour l'indic de Luc j'ai essayé de bricoler un truc avec des coeffs binomiaux mais j'ai pas encore bien cherché ..
Ca m'a l'air plutôt compliqué ! :we:
Obtenir une formule récursive donnant le n-ième terme en fonction des précédents n'est pas super difficile (et il y a effectivement des coeff. binomiaux dedans)Darkwolftech a écrit:Après pour l'indic de Luc j'ai essayé de bricoler un truc avec des coeffs binomiaux mais j'ai pas encore bien cherché ...
Je te laisse chercher un peu plus...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 78 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
