Nombre de partitions
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 13 Aoû 2009, 17:05
par lapras » 13 Aoû 2009, 17:05
Bonsoir,
est ce qu'il existe une formule connue donnant le nombre de partitions en p sous ensembles d'un ensemble à n éléments ?
Ou au moins une approximation de cette formule ?
Lapras :we:
-
xyz1975
- Membre Rationnel
- Messages: 555
- Enregistré le: 15 Sep 2007, 21:30
-
 par xyz1975 » 13 Aoû 2009, 17:34
par xyz1975 » 13 Aoû 2009, 17:34
Bonjour Lapras,
Enfin sur maths-forum tu vas bien, je ne sais pas est ce que tu te rappelles de moi ou non?
Comme réponse à ta question c'est le nombre de Bell.
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 13 Aoû 2009, 17:46
par lapras » 13 Aoû 2009, 17:46
Salut,
oui je me rappelle de toi, ca va bien ?
(je ne peux m'occuper que de ce forum, par manque de temps)
Le nombre de bell c'est juste le nombre de partitions de mon ensemble mais là je veux le nombre de partitions en p ensemble. (donc un deuxieme parametre)
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 13 Aoû 2009, 17:47
par Nightmare » 13 Aoû 2009, 17:47
Salut !
Regarde mon premier DM de sup
ici :happy3:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 13 Aoû 2009, 17:48
par Nightmare » 13 Aoû 2009, 17:48
En particulier, les nombres de Stirling.
:happy3:
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 13 Aoû 2009, 18:52
par lapras » 13 Aoû 2009, 18:52
Salut,
merci pour le fichier. J'avais trouvé cette relation de récurrencce. Le probleme c'est que j'aimerais une approximation un peu comme la formule de stirling (pour les factorielles), pour évaluer un peu ces nombres de stirling.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 13 Aoû 2009, 18:57
par Zweig » 13 Aoû 2009, 18:57
Salut,
Le nombre de partitions d'un ensemble à

éléments en

blocs vaut
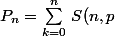p!)
avec
=\frac{1}{p!}\sum_{j=1}^{p}(-1)^{p-j}{p \choose j} j^n)
les nombres de Stirling de deuxième espèce.
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 13 Aoû 2009, 19:06
par lapras » 13 Aoû 2009, 19:06
Oui mais je ne sais pas simplifier cette formule (en faisant des approximations).
En fait mon but est de connaitre une approximation de :
S(n,1)+S(n,2)+...+S(n, [n/2])
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
