Nombre de partitions d'un ensemble de card p

[valsad]

Bonjour,

Je cherche à calculer le nombre de partions de i éléments d'un ensemble de card p. Pouvez-vous m'aider s'il vous plaît?

Merci d'avance.

[girdav]

Bonjour,
on parle de partition , mais est-ce que l'on distingue l'ordre de ces parties?
Sinon, on peut essayer de procéder par récurrence.

[valsad]

Non , on ne distingue pas l'ordre des partitions.
Il faut juste trouver le nombre de partitions de i éléments dans un ensemble de p éléments p;)i.

[alavacommejetepousse]

bonjour

c est quoi une partition de i éléments ds un ensemble de cardinal p ??

d 'après ce qu ' a écrit girdav ce serait plutôt les partitions en i classes

[valsad]

En fait je cherche à calculer le nombre de surjections d'un ensemble de p éléments vers un ensemble de i éléments.
Donc en multipliant le nombre de partition de i éléments par i, je devrais trouver mon nombre de surjection, non?

[alavacommejetepousse]

par i !; oui il se trouve qu'il n 'a y pas de formule pour les surjections seulement des relations de récurrene et des résultats simples pour des valeurs particulières de i et p : p =i , p = i+1

[charif]

bs

nonp , ça existe la formule de surjection mais c'est un problème avec un tas de questions préliminaires (parfois on le montre directement à du théorème d'inversion de pascal mais c'est hors programme )

[valsad]

Merci pour vos réponses. J'ai effectivement une relation de récurrence à démontrer. Je vais donc essayer de me débrouiller avec ça!!!...

[mathelot]

Bj,


Quand on rajoute un élément à l'ensemble E à (n-1) éléments
soit
-x vient s'ajouter à une classe de la partition
ou bien
- x se constitue en le singleton

d'où

si = nombre de partitions à éléments d'un ensemble de cardinal



somme de deux applications


Tu peux p-e essayer de descendre en reportant le décrément sur la combinaison linéaire des applications , une espèce de dualité en quelque sorte



la contrainte est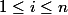
il y a moins de classes que d'éléments

[alavacommejetepousse]

bs

nonp , ça existe la formule de surjection mais c'est un problème avec un tas de questions préliminaires (parfois on le montre directement à du théorème d'inversion de pascal mais c'est hors programme )

NON définitivement il n'y a pas de formule , on peut très simplement calculer les S(n,p) de proche en proche grâce à la relation de récurrence mais c'est tout, quant à la "formule" dont tu parles fondée sur l'inversion de pascal elle n'est pas effective.

[mathelot]

NON définitivement il n'y a pas de formule , on peut très simplement calculer les S(n,p) de proche en proche grâce à la relation de récurrence mais c'est tout, quant à la "formule" dont tu parles fondée sur l'inversion de pascal elle n'est pas effective.

l'affirmation est péremptoire.A titre de comparaison, lire
l'article suivant

ici

[mathelot]

Re-bonjour,

soit le nombre de partitions d'un ensemble E de cardinal
en sous ensembles de E non vides

De manière plus abstraite
est le nombre de partitions à éléments d'un ensemble E de cardinal

j'ai la formule explicite




Elle se démontre en considérant sa formule de récurrence



et sa fonction génératrice



démo
on balance la formule de récurrence dans la série génératrice
et on transforme, comme d'hab, la formule de récurrence en dérivation
de séries

Cette formule néanmoins n'est pas nouvelle , voir par exemple

ici

j'essayerai de rédiger un pdf si ça intéresse qq1... :doh: