Polynomes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 12 Sep 2014, 20:58
par deltab » 12 Sep 2014, 20:58
pluie2 a écrit:d'accord. Donc je dois considérer m différent de 0 entier ou pas tel que Q(X)=m donc que deg(Q)=0.
donc je dois distinguer 2 cas : dans le cas où le polynome est nul soit Q(X)=m=0 alors l'ensemble des solutions est le polynome nul
et l'autre cas où il n'est pas nul ?
désolé mais j'ai vraiment du mal avec ce genre d'exos, je n'en ai que très peu fait et je n'ai jamais eu de correction
C'est tout a fait normal que tu trouves des difficultés si tu ne connais pas les propriétés élémentaires des polynômes en particulier les propriétés du degré.
Si R et T sont des polynômes non nuls de
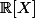
, alors deg(R+T)= 0, alors deg(P'')=n-2>=0 d'où n >= 2
2n-3=n donne n=3 Reste à vérifier s'il existe des polynômes de degré 3 solutions de l'équation.
La formule des degrés n'étant pas valable pour n<2, il faudra étudier à part les cas n=0 et n=1 et le cas où P est le polynôme nul.
-
pluie2
- Membre Rationnel
- Messages: 521
- Enregistré le: 08 Sep 2013, 13:20
-
 par pluie2 » 12 Sep 2014, 21:27
par pluie2 » 12 Sep 2014, 21:27
ok
"Comme le degré est un entier >= 0, alors deg(P'')=n-2>=0 d'où n >= 2"
comme n est supérieur à 2, j'ai au minimum affaire à un polynome de degré 2 du coup est ce que je dois écrire P=aX²+bX+c et après trouver les coeffs a,b ou c ou dois je m'arreter à seulement dire que n st supérieur à 2 ?
"2n-3=n donne n=3 Reste à vérifier s'il existe des polynômes de degré 3 solutions de l'équation." je pose P=aX^3+bX²+cX+d et comment suis je censée trouver tous les coefficients ?
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 13 Sep 2014, 00:08
par deltab » 13 Sep 2014, 00:08
pluie2 a écrit:ok
"Comme le degré est un entier >= 0, alors deg(P'')=n-2>=0 d'où n >= 2"
comme n est supérieur à 2, j'ai au minimum affaire à un polynome de degré 2 du coup est ce que je dois écrire P=aX²+bX+c et après trouver les coeffs a,b ou c ou dois je m'arreter à seulement dire que n st supérieur à 2 ?
"2n-3=n donne n=3 Reste à vérifier s'il existe des polynômes de degré 3 solutions de l'équation." je pose P=aX^3+bX²+cX+d et comment suis je censée trouver tous les coefficients ?
L'équation avec les degrés 2n-3=n n'est définie que si n est supérieur ou égal à 2, elle admet 3 >=2 comme solution, on n'a pas à étudier le cas n=2, 2 n'est pas solution de 2n-3=n.
Pour n=3 P(X)=aX^3+bX²+cX+d, calcules 18P, P', P'' et P'P'' et remplaces dans l'équation et procèdes par identification. (tu aura un système à résoudre.
Même démarche pour n=1 et n=0.
Vérifies ensuite si le polynôme est solution de l'équation, son degré ne peut être défini à partir de la définition du degré.
-
pluie2
- Membre Rationnel
- Messages: 521
- Enregistré le: 08 Sep 2013, 13:20
-
 par pluie2 » 13 Sep 2014, 12:13
par pluie2 » 13 Sep 2014, 12:13
18P=18aX^3+18bX²+18cX+18d
P'=3aX²+2bX+c
P"=6aX+2b
P'P"=18a²X^3+6abX²+12abX²+4b²X+6aX+2bc
par identification, je trouve que a=1; b=1 et c=9 donc P(X)=X^3+X²+9.
pour n=1 je dois écrire P(X)=aX+b et je fais la meme démarche ?
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 13 Sep 2014, 13:17
par deltab » 13 Sep 2014, 13:17
pluie2 a écrit:18P=18aX^3+18bX²+18cX+18d
P'=3aX²+2bX+c
P"=6aX+2b
P'P"=18a²X^3+6abX²+12abX²+4b²X+6aX+2bc
par identification, je trouve que a=1; b=1 et c=9 donc P(X)=X^3+X²+9.
Il y a une erreur de calcul dans le produit P'P".
Indépendamment de l'erreur,

n'a pas été déterminé et le polynôme P(X)=X^3+X²+9 ne correspond pas aux coefficients trouvés.
pour n=1 je dois écrire P(X)=aX+b et je fais la meme démarche ?
OUI.
-
pluie2
- Membre Rationnel
- Messages: 521
- Enregistré le: 08 Sep 2013, 13:20
-
 par pluie2 » 13 Sep 2014, 13:31
par pluie2 » 13 Sep 2014, 13:31
ok si c'est juste un problème de calcul, je devrais réussir c'était surtout la méthode qui m'interessait. merci beaucoup si j'ai un autre soucis avec ce genre de question, je vous le fais avoir (je me remets aux math ce soir et je pense avoir besoin d'une correction pour ce meme genre de calcul mais cette fois avec eds puissances de n...)
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 13 Sep 2014, 14:18
par deltab » 13 Sep 2014, 14:18
pluie2 a écrit:ok si c'est juste un problème de calcul, je devrais réussir c'était surtout la méthode qui m'interessait. merci beaucoup si j'ai un autre soucis avec ce genre de question, je vous le fais avoir (je me remets aux math ce soir et je pense avoir besoin d'une correction pour ce meme genre de calcul mais cette fois avec eds puissances de n...)
Termines l'exercice avant!
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 13 Sep 2014, 15:00
par deltab » 13 Sep 2014, 15:00
pluie2 a écrit:ok si c'est juste un problème de calcul, je devrais réussir c'était surtout la méthode qui m'interessait. merci beaucoup si j'ai un autre soucis avec ce genre de question, je vous le fais avoir (je me remets aux math ce soir et je pense avoir besoin d'une correction pour ce meme genre de calcul mais cette fois avec eds puissances de n...)
Termines l'exercice avant!
-
pluie2
- Membre Rationnel
- Messages: 521
- Enregistré le: 08 Sep 2013, 13:20
-
 par pluie2 » 13 Sep 2014, 20:25
par pluie2 » 13 Sep 2014, 20:25
si je reprends le système je trouve :
18a²=18a
18ab=18ab
4b²+6ac=18c
2bc=18d
je rtouve donc soit a=0 ou a=1. Supposons que a=1 alors b admet une infinité de solution ?
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 14 Sep 2014, 00:41
par deltab » 14 Sep 2014, 00:41
pluie2 a écrit:si je reprends le système je trouve :
18a²=18a
18ab=18ab
4b²+6ac=18c
2bc=18d
je rtouve donc soit a=0 ou a=1. Supposons que a=1 alors b admet une infinité de solution ?
La 2ème équation est erronée, c'est
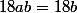
N'oublies pas que a est nul, P est un polynôme de dégré 3 donc
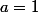
.
Comme
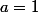
, la deuxième donne
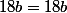
relation valable quel que soit

.
La 3ème équation devient
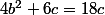
d'où
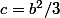
La quatrième équation devient
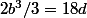
d'où
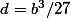
Les solutions sont donc
=X^3+bX^2 +b^2X/3 +b^3/27)
. J'ai dit "les solutions" parce qu'il n'y pas qu'une seule, elles dépendent du paramètre b.
Pour
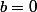
,
=X^3)
,
=3X^2)
,
=6X)
et on a bien
P''(X)=18X^3=18P(X))
-
pluie2
- Membre Rationnel
- Messages: 521
- Enregistré le: 08 Sep 2013, 13:20
-
 par pluie2 » 14 Sep 2014, 07:16
par pluie2 » 14 Sep 2014, 07:16
ok merci beaucoup je vais essayer de le refaire
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
