Polynomes

[pluie2]

Bonjour, je ne comprends pas la méthode car je pense qu'il y en a une pour déterminer tous les polynomes P de R[X] tels que :

a) P-P'=X
b) P-P'=X²
c) P-P'=X^n
d) (1-X)P'-P=X
e) (1-X)P'-P=X^n
f) XP'=P
g) P'P''=18P

j'ai essayé de faire :

a) P-P'=X
1er cas : si deg P<=1. Posons P=aX+b alors P'=a donc on a P-P'=X équivalent à aX+b-a=X soit a(X-1)=X-b
2ème cas : deg P>=2 alors on pose deg P=n>=2 soit a_n=cd(P). Si P est solution de l'équation alors: a_n-na_n=X donc a_n(1-n)=X
mais qu'en déduire ?

Ppour le reste dois je fair epareil avec X² ? mais avec les puissances de n?

merci de m'aider à comprendre :help: :help:

[Manny06]

Bonjour, je ne comprends pas la méthode car je pense qu'il y en a une pour déterminer tous les polynomes P de R[X] tels que :

a) P-P'=X
b) P-P'=X²
c) P-P'=X^n
d) (1-X)P'-P=X
e) (1-X)P'-P=X^n
f) XP'=P
g) P'P''=18P

j'ai essayé de faire :

a) P-P'=X
1er cas : si deg P=2 alors on pose deg P=n>=2 soit a_n=cd(P). Si P est solution de l'équation alors: a_n-na_n=X donc a_n(1-n)=X
mais qu'en déduire ?

Ppour le reste dois je fair epareil avec X² ? mais avec les puissances de n?

merci de m'aider à comprendre :help: :help:

d°(P-P')=d°P donc pour le a) d°P=1 P=aX+b P'=a aX+b-a=X donc a=b=1 et P=X+1

[pluie2]

bonjour,

je ne comprends pas pourquoi vous écrivez d°(P-P'), où est passé le X ?

[Manny06]

bonjour,

je ne comprends pas pourquoi vous écrivez d°(P-P'), où est passé le X ?

si P-P'=X d°(P-P')=d°X=1

[pluie2]

ok d'accord. donc ma réponse pour a) était elle incomplète ou complètement fausse ?

du coup pour b) dois je commencer pareil que pour a) puis ensuite appliquer votre résultat?

[Manny06]

ok d'accord. donc ma réponse pour a) était elle incomplète ou complètement fausse ?

du coup pour b) dois je commencer pareil que pour a) puis ensuite appliquer votre résultat?

ta réponse était incomplète car il fallait rajouter "pou tout X" ce qui donne a=1 et b=1

pour les autres P-P'=X^n
on en déduit d°P=n et le coefficient dominant an=1
ensuite tu obtiens une relation entre an et an-1 pour déterminer les coefficients par récurrence

[pluie2]

donc pour P-P'=X^n j'ai : d°P=n mais que faire du P' ? je suis désolée, je ne comprends pas comment bien rédiger

[deltab]

Bonjour.

donc pour P-P'=X^n j'ai : d°P=n mais que faire du P' ? je suis désolée, je ne comprends pas comment bien rédiger

Comme tu as pu le constater, on a à résoudre des EDO dans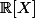 , c.à.d. trouver si elles existent des solutions polynomiales. On utilisera pour ça les propriétés des fonctions polynomiales entre autres l'écriture d'un polynôme dans la base canonique, ( 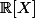est un -espace espace vectoriel) et les propriétés du degré.

[pluie2]

d'accord. Donc par exemple pour c) je ferai comme ceci ;

c) P-P'=X^n.

deg P'=deg P-1.
1er cas : si deg P<=1 alors on a P=aX+b donc P'=a donc P-P'=a(X-1)+b.
pour que X^n = a(X-1)+b seul n=0 ou n=1 marche donc P=?,?
2ème cas : Si deg P>=1 alors on note a le coefficient domunant de P donc : a-na=X^n=1 soit a(1-n)=1

?

[deltab]

d'accord. Donc par exemple pour c) je ferai comme ceci ;

c) P-P'=X^n.

deg P'=deg P-1.
1er cas : si deg P=1 alors on note a le coefficient domunant de P donc : a-na=X^n=1 soit a(1-n)=1

?

Tu as alors à distinguer les 2 cas n=0 et n=1
1) => => => donc et la solution est P(x)=1 (polynôme constant)).
2) => => => donc et , la solution est P(x)=x+1.
3) Cas général: n>1
,


En procédant par identification on obtient
et pour , .
Il reste à expliciter les coefficients pou k<n.
a_{n-1)=na_n=n
a_{n-2)=(n-1)a_{n-1)=n(n-1).
.......
On voit apparaitre la la relation pour :

[pluie2]

du coup pour la suite :

d) (1-X)P'-P=X
1 er cas : deg P<=1 donc on pose P=aX+b. ainsi, P'=a et donc (1-X)a-aX+b=X ssi a-2aX+b-X=0 donc a(1-2X)+b-x=0. J'ai l'impression que rien ne marche ici

[zygomatique]

salut

une autre méthode ....



tout d'abord si P est solution alors deg(P) = n



et on ajoute membre à membre et par télescopage

:lol3:

[pluie2]

merci zygomatique :)

avez vous une idée pour la d) ?

[zygomatique]

merci zygomatique

avez vous une idée pour la d) ?

non ... à part reprendre la méthode générale de deltab ....

[pluie2]

sauf que je suis bloquée à ce niveau :
d) (1-X)P'-P=X
1 er cas : deg P<=1 donc on pose P=aX+b. ainsi, P'=a et donc (1-X)a-aX+b=X ssi a-2aX+b-X=0 donc a(1-2X)+b-x=0. J'ai l'impression que rien ne marche ici

[Manny06]

sauf que je suis bloquée à ce niveau :
d) (1-X)P'-P=X
1 er cas : deg P<=1 donc on pose P=aX+b. ainsi, P'=a et donc (1-X)a-aX+b=X ssi a-2aX+b-X=0 donc a(1-2X)+b-x=0. J'ai l'impression que rien ne marche ici

(1-X)P'-P est la derivée de (1-X)P
donc (1-X)P=X²/2+C
pour X=1 le 1° membre est nul donc C=-1/2
il ne reste plus qu'à simplifier par (X-1)
N.B on trouve la même chose en écrivant P=anX^n+....+a1X+a0et en cherchant les coefficients an,an-1,.....a1,a0

[zygomatique]

(1-X)P'-P est la derivée de (1-X)P
donc (1-X)P=X²/2+C
pour X=1 le 1° membre est nul donc C=-1/2
il ne reste plus qu'à simplifier par (X-1)
N.B on trouve la même chose en écrivant P=anX^n+....+a1X+a0et en cherchant les coefficients an,an-1,.....a1,a0

ha oui bien vu ..

[deltab]

sauf que je suis bloquée à ce niveau :
d) (1-X)P'-P=X
1 er cas : deg P<=1 donc on pose P=aX+b. ainsi, P'=a et donc (1-X)a-aX+b=X ssi a-2aX+b-X=0 donc a(1-2X)+b-x=0. J'ai l'impression que rien ne marche ici

Il vaut mieux traiter le cas deg(P)=n et non pas deg(P)<=n.
On peut résoudre cette équation comme une équation différentielle linéaire du 1er ordre avec second membre et voir après si on a des solutions polynomiales mais on peut aussi utiliser la méthode du polynôme à coefficients indéterminés, dériver, remplacer, ..........
Pour le moment je ne peux dire laquelle des 2 méthodes est la plus rapide.

[pluie2]

je ne comprends pas cette ligne : (1-X)P=X²/2+C comment avez vous fait pour trouver l'expression de droite ?

cette méthode peut elle marcher pour e) (1-X)P'-P=X^n ?

[zygomatique]

je ne comprends pas cette ligne : (1-X)P=X²/2+C comment avez vous fait pour trouver l'expression de droite ?

cette méthode peut elle marcher pour e) (1-X)P'-P=X^n ?

dérive (1 - x)P(x) ...