Polynomes
51 messages
- Page 2 sur 3 - 1, 2, 3
j'aimerais juste revenir sur la d), j'ai compris les calculs fait mais le problème c'est que seul le cas où x=1 a été traité donc dans le cas général, quelle est l'expression du polynome à trouver?
pour la suite j'ai fait :
(1-X)P'-P=x^n
(1-x)P'-P est la dérivée de (1-X)P donc (1-X)P=x^(n+1)/(n+1)+C pour x=1 on trouve C=-1/(n+1)
mais meme problème pour le cas général
pour la suite j'ai fait :
(1-X)P'-P=x^n
(1-x)P'-P est la dérivée de (1-X)P donc (1-X)P=x^(n+1)/(n+1)+C pour x=1 on trouve C=-1/(n+1)
mais meme problème pour le cas général
pluie2 a écrit:je ne comprends pas cette ligne : (1-X)P=X²/2+C comment avez vous fait pour trouver l'expression de droite ?
cette méthode peut elle marcher pour e) (1-X)P'-P=X^n ?
puisque [(1-X)P]'=X (1-X)P est une primitive de X ensuite en faisant X=1 tu obtiens la valeur de la constante
la même méthode s'applique pour [(1-X)P]'= X^n
oui j'ai compris ceci mais je m'interroge sur ceci :
j'aimerais juste revenir sur la d), j'ai compris les calculs fait mais le problème c'est que seul le cas où x=1 a été traité donc dans le cas général, quelle est l'expression du polynome à trouver?
pour la suite j'ai fait :
(1-X)P'-P=x^n
(1-x)P'-P est la dérivée de (1-X)P donc (1-X)P=x^(n+1)/(n+1)+C pour x=1 on trouve C=-1/(n+1)
mais meme problème pour le cas général
j'aimerais juste revenir sur la d), j'ai compris les calculs fait mais le problème c'est que seul le cas où x=1 a été traité donc dans le cas général, quelle est l'expression du polynome à trouver?
pour la suite j'ai fait :
(1-X)P'-P=x^n
(1-x)P'-P est la dérivée de (1-X)P donc (1-X)P=x^(n+1)/(n+1)+C pour x=1 on trouve C=-1/(n+1)
mais meme problème pour le cas général
Bonjour
Les résolution de d) et e) telles qu'elles sont sont incomplètes.
Les calculs mènent au résultatP(X)=\dfrac{X^{n+1}}{n+1}+C) d'où
d'où =\dfrac{\dfrac{X^{n+1}}{n+1}+C}{1-X})
P est une fonction rationnelle, elle ne peut devenir polynomiale que si on peut simplifier par 1-X, et ceci nécessite que admette
admette  comme racine d'où
comme racine d'où 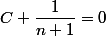 et
et 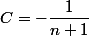 .
.
On aura alors=\dfrac{X^{n+1}-1}{(n+1)(1-X)}=\dfrac{-1}{n+1}(\dfrac{1-X^{n+1}}{1-X})=\dfrac{-1}{n+1}(1+X+X^2+\cdots+X^n))
pluie2 a écrit:oui j'ai compris ceci mais je m'interroge sur ceci :
j'aimerais juste revenir sur la d), j'ai compris les calculs fait mais le problème c'est que seul le cas où x=1 a été traité donc dans le cas général, quelle est l'expression du polynome à trouver?
pour la suite j'ai fait :
(1-X)P'-P=x^n
(1-x)P'-P est la dérivée de (1-X)P donc (1-X)P=x^(n+1)/(n+1)+C pour x=1 on trouve C=-1/(n+1)
mais meme problème pour le cas général
Les résolution de d) et e) telles qu'elles sont sont incomplètes.
Les calculs mènent au résultat
P est une fonction rationnelle, elle ne peut devenir polynomiale que si on peut simplifier par 1-X, et ceci nécessite que
On aura alors
d'accord donc à chaque fois je reprends la forme générale
pour laa suite je ne peux plus utiliser cette méthode :
f) XP'=P
g) P'P''=18P
pour XP'=P si deg P <=1 alors P=aX+b et donc aX=aX+b marche por le polynome nul si b=0 ou pour X=1 si b=0.
Pour le cas général, deg P'=deg P-1 donc le degré de P est forcément égal à 2 ?
j'ai toujours du mal avec le cas général vu la grandeur des possibilités
pour laa suite je ne peux plus utiliser cette méthode :
f) XP'=P
g) P'P''=18P
pour XP'=P si deg P <=1 alors P=aX+b et donc aX=aX+b marche por le polynome nul si b=0 ou pour X=1 si b=0.
Pour le cas général, deg P'=deg P-1 donc le degré de P est forcément égal à 2 ?
j'ai toujours du mal avec le cas général vu la grandeur des possibilités
Re.
Les relations qu'on trouve sont polynomiales, elles doivent vérifiées pour tout x. Les inconnues pour f) sont les deux coefficients a et b. Évites d'étudier les cas \le n) , mais étudies directement le cas
, mais étudies directement le cas  = n) , sinon tu auras alors distinguer le cas
, sinon tu auras alors distinguer le cas  = n) ,
, ) et
et  < n) ,
, 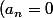) .
.
Pour g) utilises les propriétés du degré.
pluie2 a écrit:d'accord donc à chaque fois je reprends la forme générale
pour laa suite je ne peux plus utiliser cette méthode :
f) XP'=P
g) P'P''=18P
pour XP'=P si deg P <=1 alors P=aX+b et donc aX=aX+b marche por le polynome nul si b=0 ou pour X=1 si b=0.
Pour le cas général, deg P'=deg P-1 donc le degré de P est forcément égal à 2 ?
j'ai toujours du mal avec le cas général vu la grandeur des possibilités
Les relations qu'on trouve sont polynomiales, elles doivent vérifiées pour tout x. Les inconnues pour f) sont les deux coefficients a et b. Évites d'étudier les cas
Pour g) utilises les propriétés du degré.
Re.
Les relations qu'on trouve sont polynomiales, elles doivent vérifiées pour tout x. Les inconnues pour f) sont les deux coefficients a et b (les coefficients du polynôme dans le cas général). Évites d'étudier les cas \le n) , mais étudies directement le cas
, mais étudies directement le cas  = n) , sinon tu auras alors distinguer le cas
, sinon tu auras alors distinguer le cas  = n) ,
, ) et
et  < n) ,
, 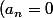) .
.
Pour g) utilises les propriétés du degré.
pluie2 a écrit:d'accord donc à chaque fois je reprends la forme générale
pour laa suite je ne peux plus utiliser cette méthode :
f) XP'=P
g) P'P''=18P
pour XP'=P si deg P <=1 alors P=aX+b et donc aX=aX+b marche por le polynome nul si b=0 ou pour X=1 si b=0.
Pour le cas général, deg P'=deg P-1 donc le degré de P est forcément égal à 2 ?
j'ai toujours du mal avec le cas général vu la grandeur des possibilités
Les relations qu'on trouve sont polynomiales, elles doivent vérifiées pour tout x. Les inconnues pour f) sont les deux coefficients a et b (les coefficients du polynôme dans le cas général). Évites d'étudier les cas
Pour g) utilises les propriétés du degré.
ok pour le f) j'ai finalement trouvé.
P'P''=18P
Je pose Q=P. Alors : soit n le degré de Q et a_n son coefficient dominant:
Q=a_nX^n+R
18Q=18(a_nX^n+R)
Q'=na_nX^(n-1)+R'
Q"=n(n-1)a_nX^(n-2)+R"
donc Q''Q'=n²(n-1)a_nX^(2n-k-1)+S avec S=(R'(n(n-1)a_nX^n+R''+R''na_nX^(n-1)+R''R') avec deg S
Comme Q"Q'-18Q=0 alors tous ses coeffs sont nuls donc n²(n-1)a_n-18a_n=0 soit n=0 ou n=1. donc Q=aX+b donc Q'Q"-18Q=(a)*0-18aX+18b=0 donc Q=18aX-18b ?
merci de me corriger
P'P''=18P
Je pose Q=P. Alors : soit n le degré de Q et a_n son coefficient dominant:
Q=a_nX^n+R
18Q=18(a_nX^n+R)
Q'=na_nX^(n-1)+R'
Q"=n(n-1)a_nX^(n-2)+R"
donc Q''Q'=n²(n-1)a_nX^(2n-k-1)+S avec S=(R'(n(n-1)a_nX^n+R''+R''na_nX^(n-1)+R''R') avec deg S
Comme Q"Q'-18Q=0 alors tous ses coeffs sont nuls donc n²(n-1)a_n-18a_n=0 soit n=0 ou n=1. donc Q=aX+b donc Q'Q"-18Q=(a)*0-18aX+18b=0 donc Q=18aX-18b ?
merci de me corriger
P'P''=18P
Je pose Q=P. Alors : soit n le degré de Q et a_n son coefficient dominant:
Q=a_nX^n+R
18Q=18(a_nX^n+R)
Q'=na_nX^(n-1)+R'
Q"=n(n-1)a_nX^(n-2)+R"
donc Q''Q'=n²(n-1)a_nX^(2n-k-1)+S avec S=(R'(n(n-1)a_nX^n+R''+R''na_nX^(n-1)+R''R') avec deg S
Comme Q"Q'-18Q=0 alors tous ses coeffs sont nuls donc n²(n-1)a_n-18a_n=0 soit n=0 ou n=1. donc Q=aX+b donc Q'Q"-18Q=(a)*0-18aX+18b=0 donc Q=18aX-18b ?
merci de me corriger
Je pose Q=P. Alors : soit n le degré de Q et a_n son coefficient dominant:
Q=a_nX^n+R
18Q=18(a_nX^n+R)
Q'=na_nX^(n-1)+R'
Q"=n(n-1)a_nX^(n-2)+R"
donc Q''Q'=n²(n-1)a_nX^(2n-k-1)+S avec S=(R'(n(n-1)a_nX^n+R''+R''na_nX^(n-1)+R''R') avec deg S
Comme Q"Q'-18Q=0 alors tous ses coeffs sont nuls donc n²(n-1)a_n-18a_n=0 soit n=0 ou n=1. donc Q=aX+b donc Q'Q"-18Q=(a)*0-18aX+18b=0 donc Q=18aX-18b ?
merci de me corriger
pluie2 a écrit:pouvez vous me corriger?
Revois l'écriture de (Q'Q'')(X) et il était inutile de poser Q=P.
Discutes directement sur le degré de P et non suivant l'expression de P selon son degré. Je m'explique: si deg(P)=n alors donc deg(P')=......... et deg(P'')=....... donc deg(P'P'')........... Compares ensuite deg(P'P'') et deg(18P')
Bonjour
D'après toi si m est un entier deg(mP)=mdeg(P) et que dire si m n'est pas un entier. Formule à revoir !!!!!!!!!
Pour P(X)=X, alors (18P)(X)=18X donc deg(P)=....... et deg(18P)=.....
La bonne formule tu la connais (ou presque), il suffit de considérer le facteur m entier ou pas comme le polynôme constant Q(X)=m (donc de degré 0).
pluie2 a écrit:ok je vois ce que vous voulelz dire mais c'est plus après :
si deg (P)=n alors deg(P')=deg(P)-1 et deg(P'')=deg(P)-2=deg(P')-1 donc deg(P'P")=deg(P')+deg(P")=deg(P)-1+deg(P)-2=2deg(P)-3
deg(18P')=18deg(P)-18>2deg(P)-3
et c'est ici que je ne sais plus comment poursuivre pour répondre au problème
D'après toi si m est un entier deg(mP)=mdeg(P) et que dire si m n'est pas un entier. Formule à revoir !!!!!!!!!
Pour P(X)=X, alors (18P)(X)=18X donc deg(P)=....... et deg(18P)=.....
La bonne formule tu la connais (ou presque), il suffit de considérer le facteur m entier ou pas comme le polynôme constant Q(X)=m (donc de degré 0).
Bonjour.
OUI
Tu l'as connais: tu as bien utilisé cette formule quand tu as écris deg(P'P'')=deg(P')+ deg(P'') (= 2deg(P)-3) ( deg(RT)=deg(R)+deg(T) si ...........)
Le "ou presque" est relatif au cas où l'un des facteurs est le polynôme nul.
Lis bien ce j'ai rappelé ((en bleu).
pluie2 a écrit:bonjour
donc en faut deg(mP)=deg(m)+deg(P)=deg(P) c'est ça la formule à revoir?
OUI
Pour P(X)=X, alors (18P)(X)=18X donc deg(P)=1et deg(18P)=18
mais après ça dépend si la formule est fausse par rapport à ce que j'ai écrit au tout début
La bonne formule tu la connais (ou presque), il suffit de considérer le facteur(entier ou pas) comme le polynôme constant Q(X)=m (donc de degré 0).
Tu l'as connais: tu as bien utilisé cette formule quand tu as écris deg(P'P'')=deg(P')+ deg(P'') (= 2deg(P)-3) ( deg(RT)=deg(R)+deg(T) si ...........)
Le "ou presque" est relatif au cas où l'un des facteurs est le polynôme nul.
Lis bien ce j'ai rappelé ((en bleu).
d'accord. Donc je dois considérer m différent de 0 entier ou pas tel que Q(X)=m donc que deg(Q)=0.
donc je dois distinguer 2 cas : dans le cas où le polynome est nul soit Q(X)=m=0 alors l'ensemble des solutions est le polynome nul
et l'autre cas où il n'est pas nul ?
désolé mais j'ai vraiment du mal avec ce genre d'exos, je n'en ai que très peu fait et je n'ai jamais eu de correction
donc je dois distinguer 2 cas : dans le cas où le polynome est nul soit Q(X)=m=0 alors l'ensemble des solutions est le polynome nul
et l'autre cas où il n'est pas nul ?
désolé mais j'ai vraiment du mal avec ce genre d'exos, je n'en ai que très peu fait et je n'ai jamais eu de correction
51 messages
- Page 2 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
