Topologie

[mathsforum]

Bonjour,
Donnons-nous un ensemble A borné non vide de R2, un point x dans A, et y dans son complémentaire. Comment alors montrer rigoureusement que le segment [x,y] rencontre le bord de A ?
Merci d'avance pour votre aide !

(J'ai considéré le point z dans [x,y] qui vérifie d(z,y)=d(y,Ainter[x,y]) (on peut le calculer explicitement), j'aurais alors voulu montrer que toute boule centrée en ce point rencontre A et le complémentaire de A, mais je n'y parviens pas)

[Ben314]

Salut,
Il y a plusieurs méthode en fonction du bagage que l'on a en topologie, mais on peut le faire de façon totalement basique : l'ensemble des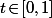 tels que est une partie non vide (0 est dedans) et majorée de donc elle admet une borne supérieure 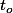. Et tu montre facilement (par exemple avec des suites) que est forcément dans la frontière de A.
Plus généralement, la même preuve montre que si tu as un arc continue (espace topologique) tel que et alors il existe 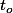tel que soit dans la frontière de .
Et si tu as plus de bagage (la notion de connexité en l'occurrence), tu peut montrer puis utiliser le Théorème dit "du passage à la douane" : dans un espace topologique, toute partie connexe qui rencontre à la fois une partie A et son complémentaire rencontre nécessairement la frontière de A.

[mathsforum]

Parfait merci beaucoup, j'ai bien compris !