Bonjour,
Je bûche sur un exercice de Topologie :
Soit
)
une suite décroissante de compacts non vides d'un espace séparé
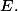
Montrer que
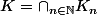
n'est pas vide et que pour tout ouvert

contenant

, il existe
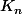
contenu dans
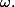
Pour la première partie de la question, je dis que tous les
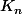
sont des parties compactes de
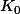
qui est compact, donc a fortiori séparé. Donc les
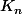
sont des fermés
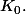
De plus, on constate que les
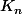
ont la propriété d'intersection finie. Donc comme
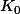
est compact,
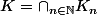
n'est pas vide.
Mais je sèche sur la deuxième partie de la question... Il faut certainement utiliser l'hypothèse «

séparé », n'est-ce pas ?
Merci d'avance pour vos suggestions !
Cordialement,
Niels.
