Topologie séparée

[Ncdk]

Bonjour,

Je dois montrer que la seule topologie séparée sur un ensemble fini est la topologie discrète.

Je sais pas trop comment montrer ça. J'ai quand même une idée, c'est de prendre une partie de X et de montrer qu'elle est fermé (Union de singletons) parce-que X est fini. Mais les singletons sont fermés si on se place dans un espace topologique séparé non ?

Dans ce que je dois montrer, est-ce que supposer que X est un espace topologique séparé et fini est valide ?

Parce-qu'en montrant qu'une partie quelconque de X est fermé, alors son complémentaire est ouvert, mais si toutes les parties de X sont fermés, alors elles sont toutes ouvertes aussi non ?

[Ben314]

Salut,
Bien que l'énoncé soit on ne peut plus clair, je comprend vraiment que dalle aux questions que tu te pose :

Je dois montrer que la seule topologie séparée sur un ensemble fini est la topologie discrète.

Je sais pas trop comment montrer ça. J'ai quand même une idée, c'est de prendre une partie de X et de montrer qu'elle est fermé (Union de singletons) parce-que X est fini. Mais les singletons sont fermés si on se place dans un espace topologique séparé non ?

Dans ce que je dois montrer, est-ce que supposer que X est un espace topologique séparé et fini est valide ?

Parce-qu'en montrant qu'une partie quelconque de X est fermé, alors son complémentaire est ouvert, mais si toutes les parties de X sont fermés, alors elles sont toutes ouvertes aussi non ?

1) Entre la première phrase en vert (le truc à montrer) et la deuxième (la question que tu te pose), je comprend pas vraiment. Quand on te demande si "toutes les blondes sont stupides", a ton avis, est-ce que c'est "valide" ou pas (comme tu dit) de commencer par chercher une blonde stupide ?
2) Le truc en bleu, c'est vrai, mais a mon avis (donc ça se discute), d'utiliser le fait qu'on sait déjà que dans un espace séparé les singletons sont fermés, c'est quand même pas très loin de dire "le résultat est vrai parce que... on sait qu'il est vrai". Donc dans un exercice aussi basique, j'aurais tendance à n'utiliser exclusivement que les définitions et rien d'autre.
3) En rouge : c'est quoi pour toi la définition de "la topologique discrète" ?

[Ncdk]

Je savais tout simplement pas si je devais me placer dans un espace topologique séparé et fini. Après coup, c'est vrai que c'est stupide comme question.

La définition de topologie discrète, je n'ai pas dans le cours, mais on m'a tout simplement dit que la topologie discrète d'un espace topologique X c'est l'ensemble des parties de X. Après je pense que c'est a moi de me poser des questions sur les éléments qui composent cette topologie.

C'est donc pour ça que si je montre (avec les hypothèses) qu'une partie quelconque de F de X est fermé, comme elles sont toutes "stockés" dans la topologie discrète, en passant par le complémentaire on montre que tout les éléments de la topologie discrète sont ouverts sous les deux hypothèses.

[Ncdk]

Du coup, m'étant repenché sur le sujet, j'avais peur d'avoir dit une bêtise sur la topologie discrète mais au final non

Du coup, si je prouve que n'importe quel sous-ensemble de X est fermé, alors c'est suffisant pour conclure ?

[Ben314]

oui.
Et tu sait (re)démontrer que, dans un espace séparé, les singletons sont fermés ?

Question bien plus difficile : la réciproque, à savoir "Si les singletons sont des fermés alors l'espace est séparée", est-elle vraie ?

[Ncdk]

Hum...

Allez je me lance. Soit X un espace topologique séparé.

Soit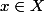 , montrer que {x} est fermé revient à montrer que X\{x} est ouvert.
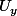Prenons , il existe et 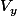des voisinages de y (Ce sont par définition des ouverts de X) tels que : et

il manque la condition que histoire d'être sur que . Je vois pas l'argument qui me permet de dire ça, mais il faut que j'ai ça, sinon je peux pas continuer.

Parce-que comme par (définition ?) et par ce qui précéde on a que et ceux pour tout y dans .

Alors on a montré que


Pour l'autre question, c'est pas un peu le but de mon exercice ? Dans le cas où X est fini la réciproque est vrai ?


EDIT : Je modifie pas ce que j'ai mit plus haut, mais j'ai compris pour l'intersection vide, c'est parce-qu'on est dans un espace séparé

[Ben314]

Hum... (comme tu dit).
Je pense qu'il faudrait que tu (re)regarde la définition de ce qu'est un espace séparé :

Prenons , il existe et des voisinages de y (Ce sont par définition des ouverts de X) tels que : et

Jusque là, c'est vaguement plus ou moins bon, modulo que :
- Ce ne sont pas tout les deux des voisinages de y, mais l'un des deux est un voisinage de x et l'autre est un voisinage de y (je pense que c'est une faute de frappe...)
- Un voisinage de x, ce n'est pas (forcément) un ouvert (ni par définition, ni par autre chose...).
Un voisinage de x, c'est (par définition) un ensemble qui contient un ouvert contenant x.
Par exemple, sur R muni de sa topologie usuelle, [-1,1] est un voisinage de 0.

Par contre, pour la suite, ça se gâte sévèrement : si un espace séparé c'était juste "un espace X pour lequel, quelque soient x et y dans X, il existe un voisinage V de x et un voisinage W de y", ben déjà ça serait très con comme définition vu que ça servirait à rien de prendre deux points et ensuite, ça servirais absolument à rien vu que dans tout espace topologique X, tout point x admet toujours au moins un voisinage, à savoir X tout entier.

Bon, bref, la définition usuelle d'espace séparé, c'est "un espace X pour lequel, quelque soient x et y distincts dans X, il existe un voisinage V de x et un voisinage W de y tels que V et W soient disjoints", (et on peut si on veut mettre "voisinage ouvert" à la place de "voisinage" vu que ça ne change rien : tout voisinage de x contient un voisinage ouvert de X et vu que ce nouveau voisinage est contenu dans l'autre, il reste disjoint du voisinage de y )

La fin, sinon, c'est bon : si l'espace est séparé alors le complémentaire d'un point s'écrit comme réunion d'ouverts.

Concernant la réciproque, effectivement, elle est vraie pour les ensembles finis vu que, si X est fini, on a les équivalences :
La topologie est discrète <=> Elle est séparée <=> Les singletons sont fermés <=> Les singletons sont ouverts.
(ce qui est complètement faux si X est infini)

Mais existe t'il des topologies (sur des ensembles infinis évidement) dans laquelle les singletons sont fermés, mais qui n'est pas séparée ?

[Ncdk]

D'accord donc si je reprend la preuve :

Soit X un espace topologique séparé.

Soit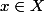 , montrer que {x} est fermé revient à montrer que X\{x} est ouvert.
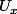Prenons , il existe et 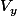des voisinages ouverts de x et y (respectivement) tels que : et .

Comme X est un espace topologique séparé on a que . Du coup ça implique (avec ce qui précède) que .

Or :
et par ce qui précède on a que et ceux pour tout y dans .

Alors on a montré que :


Pour la question, je ne sais pas, je pense que j'ai pas assez de recul sur la notion pour trouver un exemple Après je sais pas, j'avais pensé peut-être à un espace dense dans un espace topologique infini. Je sais pas, mais la séparation me fait pensé à la notion de densité, je sais pas si ça a un lien ou pas du tout.

[Ben314]

C'est tout bon, modulo que ce morceau là, à mon avis, ne va pas (c'est peut être plus un problème de Français que de math) :

...il existe et des voisinages ouverts de x et y (respectivement) tels que : et .

Comme X est un espace topologique séparé on a que ....

Tel que tu l'écrit, ça donne l'impression que l'on commence par prendre des voisinages (quelconques) de x et de y dans X, puis que, du fait que l'espace X est séparé, on en déduit qu'ils sont forcément disjoint.
Si c'était vrai, ça signifierais que tout les voisinages de x sont disjoints de tout les voisinages de y ce qui est évidement absurde vu que l'espace X tout entier est à la fois voisinage de x et de y.

Le fait que X est séparé, ça te dit qu'il existe un voisinage (ouvert si on veut) U de x et un voisinage (idem) V de y tels que U et V soit disjoints.

Sinon, pour un exemple d'espace où les singletons sont fermés, mais qui n'est pas séparé, c'est très simple (quand on a un peu "de bouteille"...) : si les singletons sont fermés, alors toutes les parties finies sont fermées (comme réunion finies de fermés) et on vérifie facilement que, sur un ensemble X quelconque, de définir les parties fermées comme étant les parties finies plus l'espace tout entier, ça défini bien une topologie sur X.
Tu peut vérifier que les axiomes marchent (évidement, si tu n'a vu que les axiomes concernant les ouverts, tu considère les parties de X soit vide, soit de complémentaire fini).
Si X est lui même fini, alors toute partie va être ouverte et fermé : c'est la topologie discrète et elle est séparée.
Par contre si X est infini, tu vérifiera aisément que la topologie ainsi défini n'est pas séparée.

Et sinon, a mon sens, il n'y a pas vraiment de lien entre la notion de séparation et la notion de densité, ne serait-ce que du fait que la notion de densité s'applique à une partie d'un espace topologique (X est dense dans Y)alors que la notion de séparation s'applique à un espace topologique (X est séparé)

[Ncdk]

Bonjour,

Merci de ta réponse, j'ai vu ce qui allait pas dans la preuve du coup, merci bien