Qui peut me donner des contre exemples pour démontrer que les propositions suivantes sont FAUSSE :
1) l'image d'un ouvert par une application continue est ouverte
2) l'image d'un fermé par une application continue est fermé
3) Une partie est compacte ssi elle est fermée et bornée
4) une partie de F est fermée ssi si toutes suite de points de F converge dans F
(J'ai un niveau DUT en maths)
Merci
Topologie; exemple
7 messages
- Page 1 sur 1
Re: topologie; exemple
Bonjour,
1) Pour l'image d'un ouvert qui n'est pas un ouvert : soit f la fonction nulle, alors=\{0\}) qui n'est pas un ouvert.
qui n'est pas un ouvert.
2) Pour l'image d'un fermé qui n'est pas un fermé, soit f la fonction inverse. Alors=]0,1]) qui n'est évidemment pas un fermé.
qui n'est évidemment pas un fermé.
3) Pour la partie compacte, le cas "fermé borné" n'est vrai que dans les espaces vectoriels normés de dimension finie. En particulier en dimension infinie, la boule unité fermée (donc bornée) n'est pas compacte.
4) Pour la 4 : je n'ai pas compris votre formulation : vous parlez d'une partie de F et de suite de points de F qui converge dans F ? Vouliez-vous dire "une partie F est fermée" ? Alors, vous pouvez certainement construire une suite dans l'intervalle qui ne converge pas : la suite qui alterne 0 et 1...
qui ne converge pas : la suite qui alterne 0 et 1...
1) Pour l'image d'un ouvert qui n'est pas un ouvert : soit f la fonction nulle, alors
2) Pour l'image d'un fermé qui n'est pas un fermé, soit f la fonction inverse. Alors
3) Pour la partie compacte, le cas "fermé borné" n'est vrai que dans les espaces vectoriels normés de dimension finie. En particulier en dimension infinie, la boule unité fermée (donc bornée) n'est pas compacte.
4) Pour la 4 : je n'ai pas compris votre formulation : vous parlez d'une partie de F et de suite de points de F qui converge dans F ? Vouliez-vous dire "une partie F est fermée" ? Alors, vous pouvez certainement construire une suite dans l'intervalle
Modifié en dernier par hdci le 11 Juil 2021, 09:30, modifié 1 fois.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: topologie; exemple
Merci
En topologie selon le livre que je lis , il est dit que :
1) l'image réciproque d'un ouvert par une application continue est ouverte
2) l'image réciproque d'un fermé par une application continue est fermé
3) Une partie compacte est fermée
Ce qui me chiffonne c'est que l'on peut faire le même raisonnement et prouver que 1) et 2) sont faux !
Je pensais qu'une partie est compacte ssi elle est fermée et bornée ! sur wiki on trouve : tout segment de ℝ est compact et, plus généralement, que les compacts de ℝ^n sont les fermés bornés.
En topologie selon le livre que je lis , il est dit que :
1) l'image réciproque d'un ouvert par une application continue est ouverte
2) l'image réciproque d'un fermé par une application continue est fermé
3) Une partie compacte est fermée
Ce qui me chiffonne c'est que l'on peut faire le même raisonnement et prouver que 1) et 2) sont faux !
Je pensais qu'une partie est compacte ssi elle est fermée et bornée ! sur wiki on trouve : tout segment de ℝ est compact et, plus généralement, que les compacts de ℝ^n sont les fermés bornés.
Re: topologie; exemple
Xavier63 a écrit:1) l'image réciproque d'un ouvert par une application continue est ouverte
2) l'image réciproque d'un fermé par une application continue est fermé
Ce qui me chiffonne c'est que l'on peut faire le même raisonnement et prouver que 1) et 2) sont faux !
Absolument pas. Les contre-exemples donnés par hdci pours l'image directe ne marchent pas du tout pour l'image réciproque. Il est bien vrai que l'image réciproque d'un ouvert (resp. fermé) par une application continue est ouverte (resp. fermée).
Pour ce qui est de :
une partie de F est fermée ssi si toutes suite de points de F converge dans F
Tu voulais dire "une partie F est fermée ssi toute suite d'éléments de F qui converge a sa limite dans F" ? Cette équivalence est fausse en général, mais elle est vraie pour les espaces métriques.
Quel est le livre que tu lis ?
Re: topologie; exemple
Parle-t-il de topologie générale ou uniquement de topologie des espaces métriques ?
S'il parle de topologie générale, tu peux considérer comme espace topologique l'ensemble des réels muni de la topologie dont les ouverts sont l'ensemble vide et les complémentaires d'ensembles (au plus) dénombrables (autrement dit, les fermés sont et les parties (au plus) dénombrables).
et les parties (au plus) dénombrables).
Quelles sont les suites convergentes dans cet espace ?
Quels sont les parties F telles que toute suite convergente d'éléments de F converge dans F ? Est-ce qu'une telle partie est toujours fermée ?
S'il parle de topologie générale, tu peux considérer comme espace topologique l'ensemble des réels muni de la topologie dont les ouverts sont l'ensemble vide et les complémentaires d'ensembles (au plus) dénombrables (autrement dit, les fermés sont
Quelles sont les suites convergentes dans cet espace ?
Quels sont les parties F telles que toute suite convergente d'éléments de F converge dans F ? Est-ce qu'une telle partie est toujours fermée ?
Re: topologie; exemple
Au passage, je vois que mes accolades autour du 0 ne sont pas sorties dans mon premier exemple ; j'ai modifié mon post en conséquence.
Comme le dit GaBuZoMeu, c'est faux, mais revenons sur la définition "usuelle" de la continuité d'une fonction réelle : une fonction est continue si elle est continue en tout et en
et en  cela s'écrit :
cela s'écrit :
-f(x_0)|<\varepsilon)
Or :
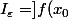-\varepsilon,f(x_0)+\varepsilon[)
Donc finalement, on a exprimé que\subset I_\varepsilon) ,
,
donc que)
L'image réciproque de l'ouvert centré en) contient un ouvert centré en
contient un ouvert centré en  donc est un voisinage de
donc est un voisinage de  .
.
Appelons alors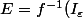) et pour chacun des
et pour chacun des 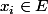 , en considérant
, en considérant 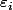 suffisamment petit pour que
suffisamment petit pour que -\varepsilon_i,f(x_i)+\varepsilon_i[\subset I_\varepsilon) on aboutit par le même raisonnement au fait que
on aboutit par le même raisonnement au fait que 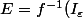) contient un voisinage de chacun des
contient un voisinage de chacun des 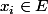 . Ainsi
. Ainsi est voisinage de chacun de ses points, par conséquent c'est un ouvert.
est voisinage de chacun de ses points, par conséquent c'est un ouvert.
Ceci étant vrai pour tout et pour tout
et pour tout 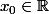 , on en déduit que l'image réciproque de tout ouvert borné est un ouvert. Comme les ouverts de
, on en déduit que l'image réciproque de tout ouvert borné est un ouvert. Comme les ouverts de  sont engendrés par les intervalles ouverts bornés, on arrive bien à la conclusion de la continuité de
sont engendrés par les intervalles ouverts bornés, on arrive bien à la conclusion de la continuité de  basée sur l'ouverture de l'image réciproque de tout ouvert.
basée sur l'ouverture de l'image réciproque de tout ouvert.
(Evidemment, pour simplifier, j'ai fait un peu l'impasse sur le cas où n'est définie que sur une partie de
n'est définie que sur une partie de  et sur le cas où
et sur le cas où  n'est pas surjective. Egalement, il faudrait montrer la réciproque, c-à-d si l'image réciproque de tout ouvert est un ouvert alors on a bien le "quel que soit epsilon etc.", mais ça c'est plus simple).
n'est pas surjective. Egalement, il faudrait montrer la réciproque, c-à-d si l'image réciproque de tout ouvert est un ouvert alors on a bien le "quel que soit epsilon etc.", mais ça c'est plus simple).
Xavier63 a écrit:En topologie selon le livre que je lis , il est dit que :
1) l'image réciproque d'un ouvert par une application continue est ouverte
[...]
Ce qui me chiffonne c'est que l'on peut faire le même raisonnement et prouver que 1) et 2) sont faux !
Comme le dit GaBuZoMeu, c'est faux, mais revenons sur la définition "usuelle" de la continuité d'une fonction réelle : une fonction est continue si elle est continue en tout
Or :
- et
Donc finalement, on a exprimé que
donc que
L'image réciproque de l'ouvert centré en
Appelons alors
Ceci étant vrai pour tout
(Evidemment, pour simplifier, j'ai fait un peu l'impasse sur le cas où
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : zwijndrecht et 42 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
