Théorème du rang en dimension infinie ?
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Gnörf
- Membre Naturel
- Messages: 51
- Enregistré le: 04 Jan 2006, 18:09
-
 par Gnörf » 29 Sep 2007, 21:05
par Gnörf » 29 Sep 2007, 21:05
Bonsoir à tous,
Désolé de poser une question comme ça mais le théorème du rang pourrait-il s'énoncer en dimension infinie ? Et si oui quel en est la bonne version ? (je n'arrive vraiment pas à trouver)
Merci !
-
quinto
- Membre Irrationnel
- Messages: 1108
- Enregistré le: 01 Mai 2005, 11:00
-
 par quinto » 29 Sep 2007, 21:10
par quinto » 29 Sep 2007, 21:10
Bonjour,
le théorème du rang n'est-il pas un corollaire du premier théorème d'isomorphisme ?
 \simeq E/ker(f))
-
Gnörf
- Membre Naturel
- Messages: 51
- Enregistré le: 04 Jan 2006, 18:09
-
 par Gnörf » 29 Sep 2007, 21:12
par Gnörf » 29 Sep 2007, 21:12
Euh ... j'ai un peu de mal à comprendre ces symboles. Est-ce que cela signifie que
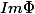
est isomorphe a tout supplémentaire de
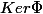
. ?
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 29 Sep 2007, 21:34
par abcd22 » 29 Sep 2007, 21:34
On peut comprendre ça comme ça (le quotient E/F d'un espace vectoriel par un sous-espace vectoriel est isomorphe à tout supplémentaire de F dans E), sauf qu'en dimension infinie pour prouver l'existence de supplémentaires il faut utiliser l'axiome du choix, c'est moins évident qu'en dimension finie, et la démonstration de
 \simeq E/\ker(f))
est plus intrinsèque que
 \simeq)
un supplémentaire de ker(f) car elle ne dépend pas du choix d'un supplémentaire particulier.
-
Gnörf
- Membre Naturel
- Messages: 51
- Enregistré le: 04 Jan 2006, 18:09
-
 par Gnörf » 29 Sep 2007, 22:01
par Gnörf » 29 Sep 2007, 22:01
Hum, en utilisant ce résultat je tombe sur une propriété qui me semble absolument fausse :
Je considère

un

ev, de dimension infinie. Soit

un endomorphisme injectif de

. On a
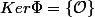
.
Le théorème du rang s'énonce :
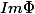
est isomorphe à tout supplémentaire de
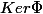
. Or on a
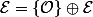
, Donc il existe un isomorphisme
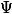
entre

et
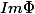
.

On a puisque

un endomorphisme :
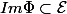

Soit
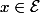
,
=y \in Im\Phi \subset \mathcal{E})
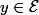
donc
 \in Im\Phi)
or
 = \Psi^{-1} (\Psi (x) ) = x)
Donc
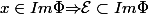
Donc
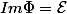
, donc

surjectif, donc

bijectif !!!!
Cherchez l'erreur !
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 29 Sep 2007, 22:13
par fahr451 » 29 Sep 2007, 22:13
Gnörf a écrit:Hum, en utilisant ce résultat je tombe sur une propriété qui me semble absolument fausse :
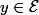
donc
 \in Im\Phi)
Cherchez l'erreur !
bonsoir elle est là
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 29 Sep 2007, 22:26
par abcd22 » 29 Sep 2007, 22:26
Gnörf a écrit:Je considère

un

ev, de dimension infinie. Soit

un endomorphisme injectif de

. On a
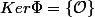
.
Le théorème du rang s'énonce :
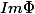
est isomorphe à tout supplémentaire de
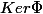
. Or on a
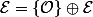
, Donc il existe un isomorphisme
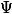
entre

et
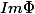
.
C'est

: on l'a supposé injectif et on a restreint l'espace d'arrivée pour qu'il soit surjectif.
-
Gnörf
- Membre Naturel
- Messages: 51
- Enregistré le: 04 Jan 2006, 18:09
-
 par Gnörf » 29 Sep 2007, 23:23
par Gnörf » 29 Sep 2007, 23:23
Euh, je ne vois plus très bien ...
si
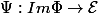
, on a pas
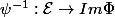
?
De plus je ne vois pas où j'ai restreint l'espace d'arrivée car il s'agit de

, qui est l'ev lui même.
Désolé j'ai vraiment du mal a visualiser mon erreur !
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 29 Sep 2007, 23:26
par fahr451 » 29 Sep 2007, 23:26
Gnörf a écrit:Soit
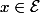
,
=y \in Im\Phi \subset \mathcal{E})
[!
avec ceci psi semble aller de E dans Im phi
et non l'inverse...
tu ne peux avoir les deux
-
Gnörf
- Membre Naturel
- Messages: 51
- Enregistré le: 04 Jan 2006, 18:09
-
 par Gnörf » 29 Sep 2007, 23:34
par Gnörf » 29 Sep 2007, 23:34
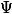
va bien de

dans
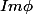
. C'est l'application inverse qui va de
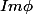
dans

(ou alors j'ai vraiment rien compris ! :marteau: )
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 30 Sep 2007, 00:00
par fahr451 » 30 Sep 2007, 00:00
si psi va de E dans Im phi
psi ^(-1) de Im phi dans E
et psi^(-1) (y) n a aucune raison d'être dans Im phi
cf mon premier message
-
Gnörf
- Membre Naturel
- Messages: 51
- Enregistré le: 04 Jan 2006, 18:09
-
 par Gnörf » 30 Sep 2007, 00:41
par Gnörf » 30 Sep 2007, 00:41
Okay ! Merci !!!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
 \simeq E/\ker(f)) est plus intrinsèque que
est plus intrinsèque que  \simeq) un supplémentaire de ker(f) car elle ne dépend pas du choix d'un supplémentaire particulier.
un supplémentaire de ker(f) car elle ne dépend pas du choix d'un supplémentaire particulier. un
un  ev, de dimension infinie. Soit
ev, de dimension infinie. Soit  un endomorphisme injectif de
un endomorphisme injectif de  . On a
. On a 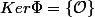 .
.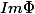 est isomorphe à tout supplémentaire de
est isomorphe à tout supplémentaire de 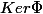 . Or on a
. Or on a 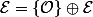 , Donc il existe un isomorphisme
, Donc il existe un isomorphisme 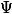 entre
entre  et
et 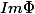 .
. On a puisque
On a puisque  un endomorphisme :
un endomorphisme : 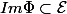
 Soit
Soit 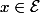 ,
, =y \in Im\Phi \subset \mathcal{E})
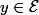 donc
donc  \in Im\Phi) or
or  = \Psi^{-1} (\Psi (x) ) = x)
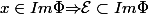
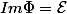 , donc
, donc  surjectif, donc
surjectif, donc  bijectif !!!!
bijectif !!!!un
ev, de dimension infinie. Soit
un endomorphisme injectif de
. On a
.
est isomorphe à tout supplémentaire de
. Or on a
, Donc il existe un isomorphisme
entre
et
.
