Theoreme d isomorphisme

[chaimaa.94]

Bon je ne sais pas comment appliquer le theoreme d isomorphisme pour resoudre ceci
On a f:G->G/f(H)
Telle que g(x)= f(x)barre
Un epimorphisme
Avec (G,*) un gpe et H un ss gpe dsitingué de G
Et f(H) aussi sous gpe distingué dans G
Montrons que G/H et G/f(H) sont isomorphe

[archimaide]

Bonjour à Tous, quelqu'un pourrait me dire (svp) comment obtient-on les nombres
16, 19, 22, 35, 37, à partir de 117 diviser par 9, svp je galère grave, a quoi correspondent ils et comment les obtient on?

117 / 9 = 13
/ 9 = 1.4444444444
/ 9 = 0.1604938272
/ 9 = 0.0178326475
/ 9 = 0.0019814053
/ 9 = 0.0002201561
/ 9 = 0.0000244618
/ 9 = 0.000002718
/ 9 = 0.000000302
/ 9 = 0.0000000336
/ 9 = 0.0000000037
/ 9 = 0.0000000004
/ 9 = 0.0000000001

[capitaine nuggets]

On a f:G->G/f(H)
Telle que g(x)= f(x)barre
Un epimorphisme

Salut !

Es-tu sûr que f est une application de G vers G/f(H) ?
Comment est définie l'application g ?
Qui est un épimorphisme ? f ou g ?

[chaimaa.94]

Ouiii g. Est l epimorphisme de G vers G/f(H)

[Ben314]

Salut,
De ce que je comprend de l'énoncé (pas clair...) , c'est :
- On se donne un groupe (G,*), un épimorphisme f:G->G, et un sous groupe H distingué de G.
- On considère le morphisme g:G->G/f(H) qui à x de G associe f(x)f(H) (sachant que, vu que f est surjective, f(H) est bien un sous groupe distingué de G)
- On voudrait montrer que g se factorise en une application de G/H->G/f(H) et que cette application est un isomorphisme de groupe.

Le fait que g se factorise en un application vien simplement du fait que et cette application est surjective vu que g l'est (car f est surjective ainsi que la projection canonique G->G/f(H)).
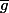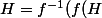Par contre, a priori, il n'y a pas de raison que soit injective vu que ça signifierais que ce qui n'est pas forcément vrai.