Bonjour,
je n'arrive pas à voir la piste à suivre pour répondre à la question suivante:
quel est le plus petit entier naturel n tel que Sn contient un sous-groupe isomorphe à chacun des groupes suivants, puis déterminer ces sous-groupes .
1) C2xC2xC2
2) D10
3) S3xS3
Merci d'avance.
Théorème de Cayley
6 messages
- Page 1 sur 1
Re: théorème de Cayley
Sous groupe, isomorphe, Cayley, j'ai complètement oublié ce que tout ça veut dire.
Mais ce que je comprends, c'est qu'on nous demande :
quel est le plus petit entier supérieur ou égal à :
2x2x2
10
3x3
Et donc la réponse est : ....
Reste à bâtir les 3 sous-groupes.
Mais ce que je comprends, c'est qu'on nous demande :
quel est le plus petit entier supérieur ou égal à :
2x2x2
10
3x3
Et donc la réponse est : ....
Reste à bâtir les 3 sous-groupes.
Re: théorème de Cayley
Non.
Par exemple, le premier groupe se plonge dans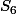 . et je crois me souvenir que
. et je crois me souvenir que  .
.
Je n'en dis pas plus : je laisse trouver le plongement, et un argument qui établit qu'on ne peut pas faire plus petit que 6.
Par exemple, le premier groupe se plonge dans
Je n'en dis pas plus : je laisse trouver le plongement, et un argument qui établit qu'on ne peut pas faire plus petit que 6.
Re: théorème de Cayley
J'ai essayé de montrer que dans les sous-groupes de Sn qui sont isomorphes à C2xC2xC2 , chaque élément doit avoir 2 pour ordre , ce qui n'est pas le cas pour les sous-groupes de S4 , ni de S5, mais je ne vois pas une démonstration claire, c'est juste intuitif, par contre pour S6 j'en ai trouvé un.
pourriez-vous m'aider plus?
pourriez-vous m'aider plus?
Re: théorème de Cayley
Il y a un moyen : chercher à quoi ressemblent les sous-groupes d'ordre 8 de 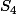 et
et 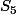 .
.
Tu connais les théorèmes de Sylow ? Ce sont des 2-Sylow dans ces groupes. Donc si tu attrapes un sous-groupe d'ordre 8 de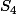 , tu sais à quoi ressemblent tous les sous-groupes d'ordre 8 de
, tu sais à quoi ressemblent tous les sous-groupes d'ordre 8 de 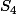 et
et 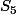 .
.
Tu connais les théorèmes de Sylow ? Ce sont des 2-Sylow dans ces groupes. Donc si tu attrapes un sous-groupe d'ordre 8 de
Re: théorème de Cayley
Le plus facile, finalement, c'est le 3 : trouver le plus petit  tel que
tel que  contient un sous-groupe isomorphe à
contient un sous-groupe isomorphe à  .
.
Les autres se traitent bien, mais avec des arguments un peu plus subtils.
Les autres se traitent bien, mais avec des arguments un peu plus subtils.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
