Ncdk a écrit: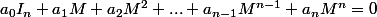
ça,
c'est (du verbe être) le théorème de Cayley-Hamilton et tu conclue que... rien d'autre que cette formule que tu peut évidement écrire
=0)
où P est le polynôme caractéristique.
Après, si ça t'intéresse tu peut en chercher des corollaires dans des cas particulier, mais le théorème, c'est "juste" ça.
Et les

ce sont les coeffs du polynôme caractéristique (regarde le début de la preuve). Il n'y a aucune raison qu'il soient nul. Le seul truc qu'on peut dire sur eux, c'est que
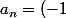^n)
(le terme dominant du polynôme caractéristique est toujours
^nX ^n)
avec la définition Française du polynôme caractéristique)
Ncdk a écrit:Le polynôme caractéristique associé à la matrice A vu qu'on a posé
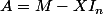
est nul Donc en gros :
=0)
par contre c'est faux de dire
=0)
?
On n'a pas du tout "posé que
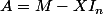
est nul" (je vois pas ce que ça veut dire d'ailleurs).
Par contre, si tu note
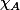
le polynôme caractéristique de la matrice A alors, effectivement tu as
=0)
(c'est le théorème que tu vient de montrer), mais je sais pas si
=0)
ou non vu que je sais pas qui est
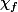
...
est nul Donc en gros :
par contre c'est faux de dire
?
