Bonjour,
Je souhaite résoudre cette exercice mais je ne sais pas par où commencer
Pouvez vous m'éclairer ?
Soit U, V dans Mn(C) montrer qu'il existe un polynôme Q de degré au plus n tel que pour tout x dans C tel que det(xU + V) =det(U) (x^n) + Q(x)
Merci d'avance
Théorème de cayley Hamilton
3 messages
- Page 1 sur 1
Re: Théorème de cayley Hamilton
Faire une récurrence sur le nombre de colonnes !
Par linéarité sur la dernière colonne :
)
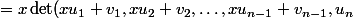)
)
Puis développer par rapport à la dernière colonne (ne contenant pas ) et appliquer l'hypothèse de récurrence.
) et appliquer l'hypothèse de récurrence.
Par linéarité sur la dernière colonne :
Puis développer par rapport à la dernière colonne (ne contenant pas
Re: Théorème de cayley Hamilton
Inutile de faire apparaître le terme ) : il suffit de voir que
: il suffit de voir que ) est un polynôme de degré inférieur à
est un polynôme de degré inférieur à  .
.
Si=ax^n+Q(x),\;Q) polynôme de degré strictement inférieur à
polynôme de degré strictement inférieur à  (il y a une erreur dans ton énoncé) tu écris
(il y a une erreur dans ton énoncé) tu écris =a+\dfrac{Q(x)}{x^n}) et tu prends la limite pour
et tu prends la limite pour 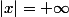 .
.
Si
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
