Merci pour la petite correction du polynôme caractéristique, donc en fait, si dans le polynôme caractéristique on prends un X scalaire ou matriciel, ça fonctionne en fait, c'est ça que tu voulais me dire par :
en remplaçant un scalaire par une matrice ça marche aussi ...
??
Ensuite,
La matrice M-X.In, c'est une matrice dont les coefficients sont en fait des polynômes en X (constant ou du premier degré) donc ta comatrice est aussi une matrice dont les coeff. sont des polynômes en X (et un mini calcul montre que ce sont des polynômes de degré au plus n-1).
En fait, je crois que la première chose qui me bloque c'est que M-Xin, c'est une matrice d'odre n, avec sur la diagonale des termes polynomiales, mais pourtant, M est une matrice qui peut comporter des éléments ailleurs que sur la diagonale non ?
Je voudrais pas dire de bêtise, mais bon je suis là pour apprendre et me tromper, mais M doit être semblable à une matrice diagonale pour utiliser ce théorème ?
Ensuite pour la deuxième partie, le petit calcul dont tu me parles c'est ça :
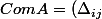)
avec
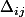
qui sont les cofacteurs de la comatrice.
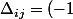^{i+j} m_{i,j})
et par définition on appelle mineur dordre
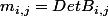
ou
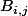
est la matrice obtenu en supprimant la ième ligne et la jième colonne donc au final c'est le principe du développement d'une matrice, du coup les termes de notre comatrice dont les coefficients sont des polynômes en X sont au plus de degrés n-1
Je trouve que ça tient pas trop la route xD
Sauf que, une matrice à coeff. des polynômes en X, tu peut l'écrire comme polynôme en X à coeff matriciels, c'est à dire sous la forme
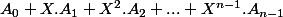
où les

sont des matrices à coefficients constants (je te laisse réfléchir au pourquoi : c'est tout con...)
Partant de là, tu n'a plus qu'à développer
En fait je vois pas pourquoi les

sont des matrices à coefficients constants, c'est juste pour dire que quand on additionne tout on retombe sur notre matrice de départ, donc que les matrices

ne dépendent pas de
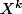
Avec k variant de 0 à n-1 ?
