Théorème de Cayley Hamilton

[benekire2]

Ouais en effet c'est assez con .. merci beaucoup night ;)

Sinon pour la 3 je viens de trouver je pense, je poste ma démo dès que je l'ai relue/corrigée , mais elle me parait bien "alambiqué" et je pense qu'il y a beaucoup plus direct.

[benekire2]

En fait j'arrive a montrer que : spectre A ={0} => A nilpotente , mais j'arrive pas a montrer que les seules valeurs propres de A sont 0. En fait je suis parti du fait que tr(A) est la somme des valeurs propres i.e que la somme des valeurs propres est nulle . J'aimerais bien avoir des relations similaires mais j'y arrive pas !

( l y avait une erreur dans ma démo .. )

EDIT. C'est bon au final ... :zen: si est valeur propre de A alors ... est valeur propre de A²

Du coup je dois résoudre :

{
{...
{

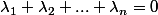
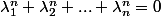
Et il se trouve que c'est un système que j'avais déjà résolu dans le passé :we: ( mais pas dans le problème .. )

N'y a-il pas plus simple ?

[Nightmare]

Vandermonde me semble être le plus simple mais ça n'a pas de rapport avec ton exercice donc ce n'est surement pas la réponse attendue. Au passage, il faut quand même distinguer le cas où toutes les valeurs propres de A sont distinctes ou non.

Pour une méthode utilisant ce que tu as déjà fait, tu peux utiliser la formule que je t'ai donnée pour C(j) en fonction des puissances de A.

Une autre méthode est d'évaluer P'(X)/P(X), en faire un DL, et de montrer que P'(x)/P(x)=n/x

[benekire2]

Oui je fais une DES de P'/P je trouve .
Par contre je développe comment pour obtenir que ça fait n/x ?

[Nightmare]

Comme je t'ai dit, fait un DL et n'oublie pas que les traces Tr(A^k) sont nulles !

[benekire2]

Oui , mais un DL en quel point ? :doh:

[Nightmare]

Au voisinage de l'infini, tu devrais trouver un truc du genre soit . Je te laisse essayer de montrer qu'on arrive ici et conclure.

[benekire2]

Oui, j'ai réussi a avoir ta formule, j'ai développé en 0 P'(1/x)/P(1/x) et j'ai trouvé.

Maintenant faut montrer que le o(1/x^(n+1)) est nul et encore une fois je ne vois pas comment procéder.

[Nightmare]

et , donc on obtient que et je te laisse conclure.

[benekire2]

Merci !

Encore une méthode bonne a connaître , je me demandais vraiment comment on pouvait s'en sortir !

Sinon pour la 4 il me faut montrer que si f,g€F alors f+g est aussi nilpotent et a priori sans a condition de commutativité. Je pense qu'on peut se servir du fait que fg et f sont aussi nilpotentes ...

[Nightmare]

Sans l'hypothèse que f et g commutent? C'est généralement faux! Contre-exemple et dans R²

[Ben314]

Oui, mais ici, on suppose que F est stable par produit, c'est à dire que le produit de deux éléments de F est dans F donc en particulier est encore nilpotent (ce qui n'est pas le cas de ton exemple).
La preuve découle assez directement de la caractérisation donnée au 3) des endomorphismes nilpotents (et du fait que la trace d'une somme est la somme des traces).

[benekire2]

Re !

En effet ça découle du 3 , pour le prouver j'ai pris A,B de F et j'ai cherché la trace de (A+B)^k
Bon , en regardant de plus près la question 3, on aurait même pu montrer l'équivalence.

[Nightmare]

Oui, mais ici, on suppose que F est stable par produit

Effectivement, je n'avais pas pris en compte cette hypothèse !