Theorème de Caratheodory !
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 23 Mar 2008, 21:48
par barbu23 » 23 Mar 2008, 21:48
Bonjour :
Est-ce que vous pouvez m'écrire ici la démonstration du théorème de Caratheodory sur l'enveloppe convexe d'un ensemble
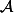
dans un espace de dimension

qui n'est autre que l'ensemble des barycentres à coefficients positifs de moins de
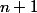
points de
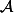
...
Ils disent qu'il y a plusieurs itérations à faire, mais je ne sais pas à quel niveau de démonstration on trouve ça ... ! ( ça c'est du pur cours ça, ça n'a rien à avoir avec la pratique ... )
Merci infiniment
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 23 Mar 2008, 21:51
par barbu23 » 23 Mar 2008, 21:51
Je cherche la version geometrique et pas algebrique avec ce genre de notations :
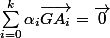
et

le barycentre !
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 23 Mar 2008, 22:00
par barbu23 » 23 Mar 2008, 22:00
l'idée, d'après ce qu'on m'a raconté cet après midi , c'est qu'on prend un point quelconque de l'enveloppe convexe ... il s'ecrit comme combinaison linéaire de

points ... si on suppose que
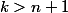
, alors le système engendré par ces points est affinement lié et on cherche ... on cherche ... jusqu'à trouver que ce point est barycentre de
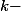
points à coefficients positifs ... en utilisant les itérations ... mais comment, je ne sais pas comment !
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 24 Mar 2008, 09:40
par ThSQ » 24 Mar 2008, 09:40
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 24 Mar 2008, 09:53
par Maxmau » 24 Mar 2008, 09:53
barbu23 a écrit:l'idée, d'après ce qu'on m'a raconté cet après midi , c'est qu'on prend un point quelconque de l'enveloppe convexe ... il s'ecrit comme combinaison linéaire de

points ... si on suppose que
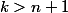
, alors le système engendré par ces points est affinement lié et on cherche ... on cherche ... jusqu'à trouver que ce point est barycentre de
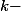
points à coefficients positifs ... en utilisant les itérations ... mais comment, je ne sais pas comment !
Soit G dans lenveloppe convexe de A
Doù : G =

1A1 +

2A2 +
..+

kAk où

i >0 et Ai dans A
Si k (n+1) les (k-1) vecteurs A1A2 , A1A3 ,
., A1Ak sont liés doù lon déduit quil existe des

i non tous nuls de somme nulle tq :


iAi = 0 ( rem :


iAi désigne le vecteur


iMAi qui est indépendant de M à cause de


i = 0 )
On écrit alors : G =

(;)i t;)i)Ai
Comme les

i ne sont pas tous nuls et de somme nulle, il en existe au moins un positif . On peut alors choisir t tel que lun des coeff

i t;)i soit nul et les autres positifs ou nuls. G est donc une CAC (CAC = combinaison affine convexe) dau plus (k-1) points de A
Si k-1 <= (n+1) terminé sinon on recommence
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 24 Mar 2008, 13:02
par barbu23 » 24 Mar 2008, 13:02
Maxmau a écrit:On écrit alors : G =

(;)i t;)i)Ai
Merci beaucoup pour toutes ces explications là ... mais , un truc que je ne sais pas encore ... comment on arrive au fait que : G =

(;)i t;)i)Ai ( svp, avec un peu plus de detail ) ..
Merci infiniment !!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 24 Mar 2008, 13:16
par barbu23 » 24 Mar 2008, 13:16
Maxmau a écrit:Soit G dans lenveloppe convexe de A
Doù : G =

1A1 +

2A2 +
..+

kAk où

i >0 et Ai dans A
Si k (n+1) les (k-1) vecteurs A1A2 , A1A3 ,
., A1Ak sont liés doù lon déduit quil existe des

i non tous nuls de somme nulle tq :


iAi = 0 ( rem :


iAi désigne le vecteur


iMAi qui est indépendant de M à cause de


i = 0 )
On écrit alors : G =

(;)i t;)i)Ai
Comme les

i ne sont pas tous nuls et de somme nulle, il en existe au moins un positif . On peut alors choisir t tel que lun des coeff

i t;)i soit nul et les autres positifs ou nuls. G est donc une CAC (CAC = combinaison affine convexe) dau plus (k-1) points de A
Si k-1 <= (n+1) terminé sinon on recommence
On additionne G =

1A1 +

2A2 +
..+

kAk et


iAi = 0 et on obtient ce que tu as ecrit "Maxmau", c'est ça ?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 24 Mar 2008, 19:42
par barbu23 » 24 Mar 2008, 19:42
Help please ! Merci !
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 24 Mar 2008, 20:36
par Maxmau » 24 Mar 2008, 20:36
barbu23 a écrit:Help please ! Merci !
Un oubli de ma part G est une CAC des Ai donc

;)i = 1 ( mais tu as certainement rectifié)
Ok mais noublie pas le t
G =

;)iAi =

;)iAi - t


iAi =

(;)i t;)i)Ai (puisque


iAi = 0)
Rem lécriture

;)iAi - t


iAi est correcte. Cest un point plus un vecteur (point translaté du point

;)iAi par le vecteur -t


iAi ). Si ce genre décriture te déroute tu vectorialises en utilisant une origine quelconque :
OG =

;)iOAi =

;)iOAi - t


iOAi =

(;)i t;)i)OAi (puisque


iOAi = 0)
 par legeniedesalpages » 24 Mar 2008, 20:47
par legeniedesalpages » 24 Mar 2008, 20:47
ThSQ a écrit:Google is your friend, wiki is your mother
:ptdr: :marteau:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
