Echantillonnage - théorème de Moivre -Laplace - théorème LC

[Pseuda]

Par exemple en 2nde, avec n25 et 0,2p0,8, on a : p et 1-p, donc l'intervalle de fluctuation est inclus dans [0,1], on est tranquille de ce côté-là.

La correction de continuité améliore pourtant bien la probabilité quand on utilise la loi normale à la place de la loi binomiale.

Si on fait le bilan de l'intérêt d'utiliser la loi normale à la place de la loi binomiale : les calculs sont plus faciles avec la loi normale, les calculs sont exacts avec la loi binomiale et seulement approchés avec la loi normale, on peut les faire avec toute valeur avec la loi normale (on est peut-être limité par les calculatrices avec la loi binomiale), on peut résoudre des équations avec la loi normale, la technique d'approximation de la loi binomiale avec la loi normale, et tout ce qui va avec, est quand même assez complexe.

Je continue à ne pas comprendre comment la probabilité peut être supérieure à 95% avec la loi binomiale quand on tronque aux valeurs entières l'intervalle de fluctuation au seuil de 95% du nombre de succès obtenu avec la loi normale.

[zygomatique]

je ne dis pas que la correction de continuité n'améliore pas les choses .... je dis simplement que c'est un correctif ... qui convient bien ... et très simple ...

on pourrait très bien choisir un correctif en ne considérant plus des rectangles mais des trapèzes ... mais c'est plus compliqué ....

quand je regarde ton tableau : et ça donne quoi pour p = 0,2 et n = 30, 31, 32 .... pour voir ....

je pense que le truc provient que lorsqu'on considère les [a/n, b/n] on travaille avec des entiers et des k/n ....et que ces k/n restent discrets même s'il y a bien contraction de 0 < k < n à 0 < k/n < 1

ce qui fait qu'il y a "des sauts" de probabilité quand on passe de k/n à (k + 1)/n ....

et quand on regarde ton tableau la borne inf est 2 pour plusieurs valeurs de n ....

il serait bien de connaître la variation de proba de P(X = k) quand on passe de n à n + 1 au voisinage de n = 29 et p = 0,2

[Pseuda]

Bonjour,

Merci zygomatique, tu m'as mise sur la voie. En effet, en prenant par exemple n=30 et p=0,2 (afin que l'intervalle de fluctuation de la loi binomiale soit centré sur la moyenne, pour ne pas rajouter une distorsion supplémentaire), on obtient les résultats suivants :

- intervalle de fluctuation de la fréquence de succès de la loi normale au seuil de 95% : [0,0568618 ; 0,3431382]
- intervalle de fluctuation du nombre de succès de la loi normale au seuil de 95% : [1,7059 ; 10,2941]
- intervalle de fluctuation du nombre de succès de la loi binomiale correspondant : [2 ; 10]
- même moyenne de 6 et même écart-type de 2,19 pour les 2 lois
- probabilité d'appartenance du nombre de succès à l'intervalle de fluctuation selon la loi binomiale : 96,39%

Les 2 bornes de l'intervalle tronqué de la loi binomiale sont comptées, et comptées sur une base de rectangle de 1, cela correspond en fait pour la loi normale à peu près (correction de continuité) à l'intervalle : [1,5 ; 10,5] plus large que l'intervalle de fluctuation de la loi normale . Une probabilité supérieure à 95% se produit dès que l'on est dans ce cas de figure : on tronque pour la loi binomiale, mais les bornes sont comptées pour 1, ce qui ré-augmente l'intervalle tronqué de 0,5 à gauche et de 0,5 à droite. Soit grosso modo, 1 chance sur 2 de se produire (d'être au-dessus de 95% ou en-dessous).

Concernant la méthode des trapèzes, quand on applique la correction de continuité, cela revient à peu près à appliquer un trapèze aux bornes de l'intervalle de la loi normale ?

Bonne journée à tous.

[Romy]

Bonjour à tous.

C'est la 1ère fois que j'ai à enseigner l'échantillonnage.

Ah! Or, la définition se retrouve pourtant dans les cours dispensés auparavant chez divers auteurs qui publient.

A propos de l'intervalle de fluctuation : le théorème de Moivre-Laplace donne un intervalle de fluctuation qui se calcule sous réserve que n soit assez grand. Obtenu grâce à une convergence, on le qualifie d'asymptotique.

Le théorème auquel on peut accéder est le suivant : si la variable aléatoire Xn suit la loi : où : ,
alors : Pour tout : où et l’unique réel tel que : , et Z sera alors la variable qui suit la loi normale : .

[Pseuda]

Bonjour,

Merci, cela résume ce qui a été dit plus haut. Mais les auteurs ne citent pas leurs sources (comme d'ailleurs la plupart des théorèmes exposés au collège et au lycée, où tout ou presque est admis). Ils citent le théorème de Moivre-Laplace pour introduire la loi normale (certainement pour justifier son intérêt par rapport à la loi binomiale). Mais là, l'intuition ne joue pas (contrairement à d'autres théorèmes) : par quel mécanisme secret une loi discrète peut se transformer en une loi continue (quand n tend vers +oo, les probas de la loi binomiale tendent individuellement vers 0) ?

Puis, avec une démonstration sortie d'un chapeau, ils introduisent les intervalles de fluctuation asymptotiques avec des restrictions sorties d'on ne sait où. Bref, on n'y comprend rien (parce qu'il faut au préalable comprendre ce théorème qui n'est pas à la portée de l'élève de TS moyen, comprendre comment une loi discrète peut tendre vers une loi continue : il faut se placer sur des intervalles, pourquoi on utilise la loi normale en lieu et place de la loi binomiale, soit quelque chose de juste par quelque chose d'approximatif et parfois faux, pourquoi on centre et réduit au préalable ces lois, d'où sortent les conditions d'applications, pourquoi on n'a pas exactement le résultat escompté, quelle est la marge d'erreur, etc....).

Pour moi, l'échantillonnage, ce sont des maths appliquées (comme il en existe tout un tas), je ne comprends pas ce que cela fait au programme du lycée.

De savoir déjà calculer avec des lois discrètes me paraît plus utile dans la vie pratique. Or cela a été supprimé ou presque du programme du lycée : quelle tristesse !

[Pseuda]

Bonjour,

A la réflexion, d'être au-dessus de 95% pour la probabilité qu'a un échantillon d'être dans l'intervalle de fluctuation des fréquences de succès, n'est pas mieux que d'être en-dessous.

En effet, si on s'est fixé comme règle d'accepter un échantillon dont la fréquence appartient à l'intervalle de fluctuation au seuil de 95% (et de le rejeter sinon) :
- si l'intervalle de fluctuation contient en réalité moins de 95% des fréquences (entre 94% et 95%), on risque de rejeter à tort un échantillon conforme,
- si l'intervalle de fluctuation contient en réalité plus de 95% des fréquences (entre 95% et 96%), on risque d'accepter à tort un échantillon non conforme.

C'est pas mieux. Quel est le plus grave ? Je ne saurais dire, cela doit dépendre du contexte dans lequel on fait le test, n'est-ce pas ce que tu voulais dire, zygomatique ?

Du coup, l'intervalle de fluctuation de 2nde, qui contient en réalité très rapidement plus de 95% des fréquences quand n croit, (de 98% à 99% dès n=25 pour p = 0,2) est très approximatif, bien plus que celui de terminale (évidemment), sauf si p va vers 0,5 (on rejoint l'intervalle de terminale).

Autre remarque : plutôt que de calculer un intervalle de fluctuation, on pourrait aussi calculer directement, face à une fréquence observée dans un échantillon, la probabilité qu'avait cet échantillon de contenir ce nombre de succès au moins (si ce nombre est > à la proportion supposée), ou au plus (sinon), et il ne faudrait pas (pour accepter cet échantillon) que cette probabilité soit < à 2,5% (ou /2), zone de rejet. Avec la loi binomiale . Ouf !

Lien intéressant, qui lui-même renvoie à d'autres liens intéressants :
http://www.les-mathematiques.net/phorum ... 460,647927

Et aussi : http://eduscol.education.fr/cid45766/ma ... lycee.html (probabilités et statistiques)

[zygomatique]

C'est pas mieux. Quel est le plus grave ? Je ne saurais dire, cela doit dépendre du contexte dans lequel on fait le test, n'est-ce pas ce que tu voulais dire, zygomatique ?

je ne sais plus à quel sujet ... je voulais dire quoi !! ... cependant deux remarques :

1/ je ne vois pas l'intérêt de travailler avec cet intervalle de fluctuation aussi imprécis si ce n'est dès la seconde leur apprendre à faire des tests d'hypothèse (le principe général)

2/ car :

a/ je pense qu'il y a bien d'autre chose à faire en seconde ...

b/ commencer en première avec la loi binomiale directement et l'intervalle [a/n, b/n] me semble bien suffisant d'autant plus qu'il n'y a aucune condition sur n et p

cependant f = X/n reste toujours discrète et on reste toujours "à environ 95%"

[Pseuda]

Bonsoir,

C'est cela :

je dirais que ce n'est pas temps le 95% ou un peu moins qui importe ni même le "asymptotique" quand on travaille avec n = 30 ou 50 ...

dans mes cours je dis toujours "à environ 95%" et je travaille essentiellement avec des exemples où n reste supérieure à la cinquantaine pour minimiser l'erreur .... (afin que les résultats aient un minimum de sens)

mais c'est plutôt de pb plus général de notre education/instruction : quel est l'objectif de faire étudier telle ou telle notion et quel "socle minimal" voulons-nous apporter à un jeune pour qu'il soit apte à se débrouiller tout seul par la suite ....

et bâtir sur du sable n'est pas la meilleure solution ... il y a mieux à faire lorsqu'on voit le taux d'illettrisme ou la faiblesse de calcul élémentaire (exemple flagrant : la notion même de proportionnalité, les phénomènes linéaires sont tellement mal maitrisés ...)

cependant la statistique inférentielle est un outil très puissant ... lorsqu'il est utilisé avec rigueur et que l'on sait de quoi l'on parle ... et très utilisé par l'industrie ...

ainsi savoir que c'est à peu près 95% n'est même plus important en soit ...

ce qui est important c'est de savoir construire un test pour répondre à une question ... encore faut-il se poser la bonne question et savoir si un test me permettra de prendre la bonne décision "au risque de t%" ... (ou presque t%)

C'était par rapport à l'importance de les faire réfléchir au contexte du test, plus que celle de la véracité du 95%. Les élèves sentent bien que tout cela est un peu flou. Des fois c'est : plus que 95%, d'autres, c'est : environ 95%, d'autres : entre 94 et 96%.
Cela n'aide pas à les faire comprendre, à s'approprier un concept, juste à les confirmer dans l'opinion générale : les statistiques et les chiffres, on peut leur faire dire n'importe quoi.

C'est dommage car le sujet est intéressant, voire très, mais assez complexe, mais ne me paraît pas à portée d'un lycéen, à part leur faire appliquer bêtement une formule toute faite qu'ils ne comprennent pas.

1/ je ne vois pas l'intérêt de travailler avec cet intervalle de fluctuation aussi imprécis si ce n'est dès la seconde leur apprendre à faire des tests d'hypothèse (le principe général)

2/ car :

a/ je pense qu'il y a bien d'autre chose à faire en seconde ...

b/ commencer en première avec la loi binomiale directement et l'intervalle [a/n, b/n] me semble bien suffisant d'autant plus qu'il n'y a aucune condition sur n et p

cependant f = X/n reste toujours discrète et on reste toujours "à environ 95%"

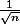
Entièrement d'accord. L'intervalle de fluctuation de 2nde n'a pas un grand intérêt du point de vue mathématique, (à part le ). Il n'est là que pour les faire réfléchir sur des tests d'hypothèse.
Mais pour ça, ils ont eu le théorème de Thalès et de Pythagore au collège : théorème direct, réciproque, contraposée... : si le triangle est rectangle, alors ..., et comme on n'a pas ..., alors ...

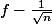
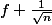
L'intérêt de l'intervalle de 2nde serait de donner un résultat simple pour l'intervalle de confiance : [,] (par résolution d'inéquations), mais là encore cet intervalle est faux (concernant l'appartenance de p cherchée à cet intervalle : mais là au moins on ne le dit pas), mais on parle de "fourchette de sondage".
A plusieurs titres :
- il est tiré d'un intervalle faux, cela n'augure pas de sa véracité, sauf heureux hasard,
- il est assorti de restrictions qui sont fausses : n30, nf5 et n(1-f)5 : que faire du cas où f est très petit, par exemple f=0,05, n=100, les conditions sont vérifiées, mais l'intervalle tombe dans une valeur <0 à gauche : la probabilité est tronquée ?
- ce n'est pas parce que la fréquence observée f appartient à l'intervalle de fluctuation centré en p avec une certaine probabilité, que la proportion p d'une loi binomiale appartient à l'intervalle de confiance centré en f avec cette même probabilité ; le problème a l'air plus compliqué que cela.

Tout cela pour dire : faut-il leur apprendre des choses fausses/approximatives pour les faire réfléchir ? Je ne pense pas. Il y a d'autres moyens.

Et aussi, pour les intéressés :
http://www.univ-irem.fr/IMG/pdf/prolong ... _henry.pdf

[Pseuda]

Bonjour,

Une dernière remarque, qui est elle aussi passée sous silence dans le programme du lycée, et je m'arrêterai là.
Désolée d'utiliser ce forum pour y mettre mes réflexions personnelles concernant ce sujet, mais cela m'aide bien à dépatouiller tout cela.

Quand on modélise une variable aléatoire X tirée de la vie courante (calibre d'une tomate, taille d'un groupe de personnes, consommation d'eau journalière...), qui la plupart du temps, prend des valeurs positives, par une loi de probabilité définie sur R (par exemple une loi normale N(,²)), encore faut-il s'assurer que la probabilité P(X<0) est très petite (de préférence inférieure à ou ), sinon la probabilité P(X>0) au lieu d'être égale à 1, événement certain, se retrouve inférieure à 1. Que fait-on dans ce cas de la probabilité résiduelle ?

Par exemple, si X suit la loi normale N(,²), on a : P(X<0)=P(Z<- / ), avec Z qui suit N(0,1), qui est loin d'être négligeable si est proche de 0, ou grand. Pour une consommation journalière d'eau (en million de litres) modélisée par une loi normale N(4 ; 2,8), on a : P(X>0) 92%. On n'a plus affaire à une loi de probabilité...

Bon on sait bien que les énoncés ne sont pas faits pour résoudre des problèmes tirés de la vie courante, mais au contraire, pour pouvoir appliquer les formules apprises dans le cours, mais cela vaudrait quand même la peine d'être DIT. (dans le même registre que les restrictions d'applications sur n et p du théorème de Moivre-Laplace).