P(X_n>n) tend vers 1 donc P(Xn tend vers +inf) = 1?
15 messages
- Page 1 sur 1
P(X_n>n) tend vers 1 donc P(Xn tend vers +inf) = 1?
Bonjour,
Dans un exercice, j'obtiens que la limite de P(X_n>n) est 1
((X_n) est une suite de variables aléatoires à valeurs dans N).
Je me demande si on peut conclure que la probabilité que X_n tend vers + infini vaut 1.
ça me paraît intuitif mais je ne vois pas comment le prouver précisément.
En effet (Xn tend vers +inf) ne s'exprime pas en fonction de X_n >n , le n étant "fixé" dans "X_n >n".
Est-ce que quelqu'un a une idée? a moins que ma conjecture soit fausse sans davantage d'hypothèses?
Merci et bonne journée
Dans un exercice, j'obtiens que la limite de P(X_n>n) est 1
((X_n) est une suite de variables aléatoires à valeurs dans N).
Je me demande si on peut conclure que la probabilité que X_n tend vers + infini vaut 1.
ça me paraît intuitif mais je ne vois pas comment le prouver précisément.
En effet (Xn tend vers +inf) ne s'exprime pas en fonction de X_n >n , le n étant "fixé" dans "X_n >n".
Est-ce que quelqu'un a une idée? a moins que ma conjecture soit fausse sans davantage d'hypothèses?
Merci et bonne journée
Re: P(X_n>n) tend vers 1 donc P(Xn tend vers +inf) = 1?
Il faudrait un énoncé clair /précis.
Mais je pense que tu as donné le bon argument : n étant fixé , ça ne va pas.
Mais je pense que tu as donné le bon argument : n étant fixé , ça ne va pas.
Re: P(X_n>n) tend vers 1 donc P(Xn tend vers +inf) = 1?
Merci pour ta réponse, X_n est la somme de VA independantes et identiquement distribuées de type Rademacher (à valeurs dans {-1,1}) et on obtient que si la loi n'est pas uniforme, par exemple pour P(Y_k=1)=p>1/2, alors P(X_n> f(n)) tend vers 1 ou f(n)=(2p-1-eps)*n avec eps>0 fixé. (par loi faible des grands nombres
Intutivement on voudrait dire que X_n tend vers +infini, mais je ne sais pas vraiment comment le montrer.
En revenant au petit w pour écrire bien l'évènement X_n(w) tend vers +infini, mais ça ne donne pas grand chose.
C'est un peu la différence loi faible/loi forte il me semble. Mais bon sinon dans l'idéal serait un contre-exemple
Intutivement on voudrait dire que X_n tend vers +infini, mais je ne sais pas vraiment comment le montrer.
En revenant au petit w pour écrire bien l'évènement X_n(w) tend vers +infini, mais ça ne donne pas grand chose.
C'est un peu la différence loi faible/loi forte il me semble. Mais bon sinon dans l'idéal serait un contre-exemple
Re: P(X_n>n) tend vers 1 donc P(Xn tend vers +inf) = 1?
J'aimerais t'aider mais je ne sais plus le faire.
Étant donné une suite de va (Xn,En) , la suite (Xn) est aussi une va sur Pi des En muni de la probabilité conjointe.
Ça je sais.
Donc parmi les valeurs prises par (Xn) ou encore les réalisations de (Xn), certaines sont des suites qui tendent vers +l'infini. Leur ensemble est un évènement dont tu supposes et aimerais démontrer que sa propa est égale à 1 compte tenu de l'énoncé.
Ce que je ne sais plus faire, c'est exprimer cet évènement en termes d'intersections et d'union,ie dans la tribu engendrée par (Xn) sur Pi des En.
Au secours les Pros!!!!!!!
Étant donné une suite de va (Xn,En) , la suite (Xn) est aussi une va sur Pi des En muni de la probabilité conjointe.
Ça je sais.
Donc parmi les valeurs prises par (Xn) ou encore les réalisations de (Xn), certaines sont des suites qui tendent vers +l'infini. Leur ensemble est un évènement dont tu supposes et aimerais démontrer que sa propa est égale à 1 compte tenu de l'énoncé.
Ce que je ne sais plus faire, c'est exprimer cet évènement en termes d'intersections et d'union,ie dans la tribu engendrée par (Xn) sur Pi des En.
Au secours les Pros!!!!!!!
Re: P(X_n>n) tend vers 1 donc P(Xn tend vers +inf) = 1?
Bonjour,
C'est une application assez immédiate de la loi forte des grands nombres.
Que dit-elle pour la suite de variables aléatoires) ?
?
C'est une application assez immédiate de la loi forte des grands nombres.
Que dit-elle pour la suite de variables aléatoires
Re: P(X_n>n) tend vers 1 donc P(Xn tend vers +inf) = 1?
Bonsoir,
Mon pb ne fait référence qu'au premier message d'actéon ie
Si lim p(Xn>n) =1 , alors p(lim Xn=+ ) =1
) =1
Mon pb ne fait référence qu'au premier message d'actéon ie
Si lim p(Xn>n) =1 , alors p(lim Xn=+
Re: P(X_n>n) tend vers 1 donc P(Xn tend vers +inf) = 1?
Je répondais à la question d'acteon, pour les  de son exercice.
de son exercice.
Re: P(X_n>n) tend vers 1 donc P(Xn tend vers +inf) = 1?
Bonjour GaBuZoMeu,
Pourrais tu avoir l'amabilité de m'aider pour:
"Ce que je ne sais plus faire, c'est exprimer cet évènement en termes d'intersections et d'union,ie dans la tribu engendrée par (Xn) sur Pi des En."
(dans mon premier message).
Pourrais tu avoir l'amabilité de m'aider pour:
"Ce que je ne sais plus faire, c'est exprimer cet évènement en termes d'intersections et d'union,ie dans la tribu engendrée par (Xn) sur Pi des En."
(dans mon premier message).
Re: P(X_n>n) tend vers 1 donc P(Xn tend vers +inf) = 1?
Bonjour tournesol,
Tu écris, avec des quantifications sur les entiers, la formule qui dit que la suite) tend vers
tend vers  et tu transformes les quantifications existentielles en réunion et les quantifications universelles en intersection.
et tu transformes les quantifications existentielles en réunion et les quantifications universelles en intersection.
Mais on peut très bien avoir=1) et en même temps
et en même temps =0) .
.
Indice pour un exemple : travailler sur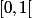 avec la mesure de probabilité uniforme et une suite de variables aléatoires
avec la mesure de probabilité uniforme et une suite de variables aléatoires _{n\geq 1}) sur cet espace probabilisé telles que
sur cet espace probabilisé telles que 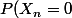=1/n) et
et =1-1/n) .
.
Tu écris, avec des quantifications sur les entiers, la formule qui dit que la suite
Mais on peut très bien avoir
Indice pour un exemple : travailler sur
Re: P(X_n>n) tend vers 1 donc P(Xn tend vers +inf) = 1?
Tout d'abord merci.
Si je te demandes de l'aide, c'est parceque j'ai essayé de faire exactement ce que tu me demandes de faire dans la première partie de ton message .
Quand aux exemples j'avais l'intension de travailler sur :
=0) et pour k>n
et pour k>n =\frac{6}{\pi^2}\frac{1}{(k-n)^2})
Si je te demandes de l'aide, c'est parceque j'ai essayé de faire exactement ce que tu me demandes de faire dans la première partie de ton message .
Quand aux exemples j'avais l'intension de travailler sur :
Re: P(X_n>n) tend vers 1 donc P(Xn tend vers +inf) = 1?
C'est pourtant simple :

devient
>p\})
Tu te compliques beaucoup la vie pour l'exemple (et je parie que tu n'aboutiras pas avec ce que tu proposes), mais tu fais comme tu veux !
devient
Tu te compliques beaucoup la vie pour l'exemple (et je parie que tu n'aboutiras pas avec ce que tu proposes), mais tu fais comme tu veux !
Re: P(X_n>n) tend vers 1 donc P(Xn tend vers +inf) = 1?
Ne laissons pas ce fil terminer en queue de poisson.
Soit donc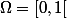 avec la mesure de probabilité uniforme.
avec la mesure de probabilité uniforme.
Pour tout entier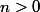 , soit
, soit  la variable aléatoire sur
la variable aléatoire sur  définie par
définie par =0) si
si 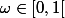 est la partie fractionnaire d'un réel de
est la partie fractionnaire d'un réel de 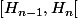 (où
(où 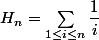 est le nombre harmonique d'indice
est le nombre harmonique d'indice  ), et
), et =n) sinon.
sinon.
On a alors=1-\dfrac1n) , quantité qui tend vers 1 quand
, quantité qui tend vers 1 quand  tend vers l'infini.
tend vers l'infini.
Par contre, pour tout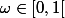 , il existe une infinité d'entiers
, il existe une infinité d'entiers  tels que
tels que =0) puisque la série harmonique diverge. Donc l'ensemble des
puisque la série harmonique diverge. Donc l'ensemble des 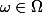 tels que la suite
tels que la suite )_{n\geq 1}) tende vers
tende vers  quand
quand  tend vers l'infini est vide. Par conséquent,
tend vers l'infini est vide. Par conséquent, =0) .
.
Morale : se méfier de ce qui semble intuitif !
Bon réveillon !
Soit donc
Pour tout entier
On a alors
Par contre, pour tout
Morale : se méfier de ce qui semble intuitif !
Bon réveillon !
Re: P(X_n>n) tend vers 1 donc P(Xn tend vers +inf) = 1?
Pour les  de l'énoncé d'Acteon, la loi forte des grands nombres montre que la suite
de l'énoncé d'Acteon, la loi forte des grands nombres montre que la suite ) converge presque sûrement vers
converge presque sûrement vers  (puisque
(puisque ) converge presque sûrement vers
converge presque sûrement vers 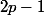 , l'espérance de
, l'espérance de 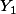 ).
).
Re: P(X_n>n) tend vers 1 donc P(Xn tend vers +inf) = 1?
Merci pour ce joli contre exemple .
Bonne et heureuse année 2023.
Bonne et heureuse année 2023.
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 84 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
