Système différentiel

[Anonyme]

on donne le système différentiel (S), où x, y et z sont trois fonctions dérivables sur R :
(S) : x'(t)=-y(t)+z(t)
y'(t)=x(t)-z(t)
z'(t)=-x(t)+y(t)

Donner les solutions complexes, puis réelles de (S).

Ce que j'ai fait :
j'ai appelé X la matrice colonne (x y z)
X' la matrice colonne (x' y' z')

J'ai donc X' = AX

J'ai cherché les valeurs propres de A (0 ; 3i ; -3i)

Mais après je suis bloqué...

[Zebulon]

Bonsoir, je te fais confiance pour les valeurs propres. Diagonaliser la matrice est la bonne méthode. Cela te donne:

donc X est solution de ton premier système différentiel si et seulement si ssi 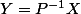est solution du nouveau système Y'=DY qui se résout très facilement... :happy2: Après tu reviens à X et c'est gagné!
Bon courage et à bientôt,
Zeb.

[Anonyme]

je suis OK avec ce que tu m'as écrit...seulement je n'arrive pas à trouver P