Suites réelles

par **zap21** » 30 Sep 2010, 18:52

Bonsoir à tous,

J'ai reçu un devoir en mathématique à rendre pour le 12 octobre au plus tard. Je viens de potasser deux heures sur le problème sans trouver une réelle ouverture pour commencer à la résoudre. J'en viens donc à demander votre aide.

Voici l'énoncé:

Il faudrait donc réussir à exprimer (u)n en fonction de n. Chose que je n'arrive pas à faire.

par **windows7** » 30 Sep 2010, 18:53

c'est une blague ?

par **zap21** » 30 Sep 2010, 18:54

Euh non, pourquoi ? :hein: :triste:

par **windows7** » 30 Sep 2010, 18:55

bah ca y ressemble ..

par **zap21** » 30 Sep 2010, 18:55

Et pourquoi ? Je demande pas de me faire l'exercice, mais un indice me serait fort utile.

par **windows7** » 30 Sep 2010, 18:58

un indice de taille alors, ca veut dire quoi Un bien definie ?

par **Doraki** » 30 Sep 2010, 18:58

où est-ce quet 'as lu qu'on te demandait de trouver une expression de un en fonction de n ?

par **zap21** » 30 Sep 2010, 19:00

Je ne sais pas vraiment ce que veut dire "bien défini". On a reçu l'énoncé mais aucune explication :triste:

Et pour le fait d'exprimer (u)n en fonction de n, c'est ce qu'on avait dans les exercices précédents, donc j'ai supposé qu'on devait faire de cette manière là. Maintenant si vous me dites que ce n'est pas ça, je vous crois :p

par **zap21** » 30 Sep 2010, 19:17

Pas très accueillant sur ce forum. Merci de l'aide quand même.

par **Ben314** » 30 Sep 2010, 19:27

Bon,
Reprenons le B-A-BA pour montrer qu'on est pas des "BOEUF".
Dire qu'une expression est "bien définie", ben, comme son nom l'indique, ça veut dire que... on peut faire le calcul.
Par exemple 1/x n'est pas bien défini lorsque x=0 et racine(x) n'est pas bien défini lorsque x=-3.
Ici la formule qui définie U(n+1) contient 1/Un, ce qui signifie que, pour pouvoir calculer U(n+1), ben il faut que Un soit non nul. Donc, il faut montrer que Un est non nul pour justifier que l'on peut calculer le suivant.

En fait, comme c'est super façile à montrer, on montre (par récurence évidement, vu que la suite est définie... par récurence) que Un est supérieur à 1 (et donc que l'on peut calculer U(n+1).

par **Pythales** » 30 Sep 2010, 19:30

La relation s'écrit

soit

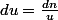
ce qui donne

à déterminer par les conditions initiales.

par **zap21** » 30 Sep 2010, 19:31

Merci de ta réponse Ben314. Et comment dois-je m'y prendre pour démonter cela ? Je dois exprimer (u)n en fonction de n ou ce n'est pas du tout nécessaire ?

par **zap21** » 30 Sep 2010, 19:34

Pythales j'avoue ne pas suivre tout le raisonnement que tu as noté :hein: mais merci de l'aide.

par **Ben314** » 30 Sep 2010, 19:44

zap21 a écrit:Merci de ta réponse Ben314. Et comment dois-je m'y prendre pour démonter cela ? Je dois exprimer (u)n en fonction de n ou ce n'est pas du tout nécessaire ?

Ben, à priori, dans un exo de math, lorsque l'on ne te demande pas de faire un calcul, ben tu le fait pas.
Ici, pour montrer (par récurrence : je le redit...) que Un>=1, il n'est absolument pas utile de connaitre la formule exacte de Un.
(En plus, ça m'étonnerais fort que tu la trouve la formule qui donne Un en fonction de n : il va falloir que tu fasse tout l'exercice sans...)

par **zap21** » 30 Sep 2010, 20:42

Ok ben314. Mais saurais-tu me donner un indice pour commencer l'exercice ?

Suites réelles

Suites réelles

Qui est en ligne