Suite récurrente
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 20 Déc 2014, 15:01
par adamNIDO » 20 Déc 2014, 15:01
Bonjour,
s'il vous plait votre aide

merci pour votre aide
-
BiancoAngelo
- Membre Rationnel
- Messages: 585
- Enregistré le: 12 Déc 2011, 23:06
-
 par BiancoAngelo » 20 Déc 2014, 15:29
par BiancoAngelo » 20 Déc 2014, 15:29
adamNIDO a écrit:Bonjour,
merci pour votre aide
C'est bien

dans la définition ? Si c'est bien le cas, ça donne :
On a donc
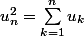
Donc que
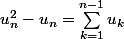
Donc on peut définir par récurrence :
Donc que
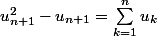
(avec
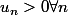
)
Sauf que :
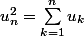
Donc
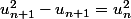
(
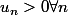
))
On peut résoudre
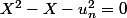
et toujours prendre la solution positive.
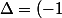^2 - 4 \times 1 \(- u_n^2) = 1 + 4 u_n^2)
Donc on a
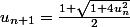
.
On peut même écrire
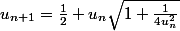
.
Ce qui donne
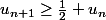
Par sommation, on obtient :
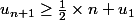
pareil que
 + 1)
ce qui montre que
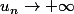
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 20 Déc 2014, 15:50
par adamNIDO » 20 Déc 2014, 15:50
BiancoAngelo a écrit:C'est bien

dans la définition ? Si c'est bien le cas, ça donne :
On a donc
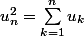
Donc que
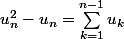
Donc on peut définir par récurrence :
Donc que
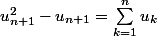
(avec
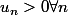
)
Sauf que :
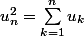
Donc
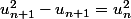
(
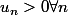
))
On peut résoudre
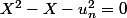
et toujours prendre la solution positive.
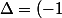^2 - 4 \times 1 \(- u_n^2) = 1 + 4 u_n^2)
Donc on a
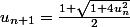
.
On peut même écrire
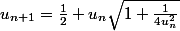
.
Ce qui donne
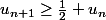
Aucune idée
-
BiancoAngelo
- Membre Rationnel
- Messages: 585
- Enregistré le: 12 Déc 2011, 23:06
-
 par BiancoAngelo » 20 Déc 2014, 15:52
par BiancoAngelo » 20 Déc 2014, 15:52
J'ai complété le post.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 20 Déc 2014, 15:57
par zygomatique » 20 Déc 2014, 15:57
adamNIDO a écrit:Bonjour,
s'il vous plait votre aide

merci pour votre aide
salut
de façon plus minimaliste
tu peux remarquer que pour tout n u_n > 1 (par récurrence)
puis
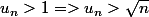
(par récurrence)
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
BiancoAngelo
- Membre Rationnel
- Messages: 585
- Enregistré le: 12 Déc 2011, 23:06
-
 par BiancoAngelo » 20 Déc 2014, 16:01
par BiancoAngelo » 20 Déc 2014, 16:01
zygomatique a écrit:salut
de façon plus
minimalistetu peux remarquer que pour tout n u_n > 1 (par récurrence)
puis
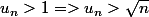
(par récurrence)
Tu m'étonnes ! :ptdr: Bien vu.
Moi j'ai vraiment fait l'étude de la suite, je voulais voir ce que c'était :we:
-
BiancoAngelo
- Membre Rationnel
- Messages: 585
- Enregistré le: 12 Déc 2011, 23:06
-
 par BiancoAngelo » 20 Déc 2014, 16:13
par BiancoAngelo » 20 Déc 2014, 16:13
Du coup, vu que
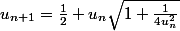
.
Et que
)
On a
^2)
Donc
^2}})
Donc
^2}})
Donc
^2}})
Et on voit bien l'équivalent arriver du coup.
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 20 Déc 2014, 16:24
par adamNIDO » 20 Déc 2014, 16:24
zygomatique a écrit:salut
de façon plus minimaliste
tu peux remarquer que pour tout n u_n > 1 (par récurrence)
puis
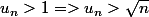
(par récurrence)
au sense stricte linegalité car u_1=1
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 20 Déc 2014, 16:30
par adamNIDO » 20 Déc 2014, 16:30
BiancoAngelo a écrit:Tu m'étonnes ! :ptdr: Bien vu.
Moi j'ai vraiment fait l'étude de la suite, je voulais voir ce que c'était :we:
de plus
on voit que

on montre d'abord par récurrence sur n :

pour n=1
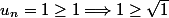
donc vraie pour 1
supposons que P est vraie pour n et montrons qui reste vrai pour n+1
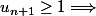
je bloque ici
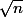
est diverge vers

donc

l'est aussi
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 20 Déc 2014, 17:50
par adamNIDO » 20 Déc 2014, 17:50
je pense que la suite doit etre definie jusqu'a n-1 et pas n
-
BiancoAngelo
- Membre Rationnel
- Messages: 585
- Enregistré le: 12 Déc 2011, 23:06
-
 par BiancoAngelo » 20 Déc 2014, 17:56
par BiancoAngelo » 20 Déc 2014, 17:56
adamNIDO a écrit:je pense que la suite doit etre definie jusqu'a n-1 et pas n
Le problème dans le fait d'utiliser la récurrence, c'est que celle-ci doit être assez explicite pour qu'on puisse l'utiliser, ce qui n'est pas trop le cas ici, à moins que je sois aveugle (ce qui est possible :ptdr: ).
Donc c'est pour ça que dans ce que j'ai écrit dès le départ, tu as le développement qui te permet de montrer ce qui est demandé. Ce n'est peut-être pas le plus court chemin, certes...
-
BiancoAngelo
- Membre Rationnel
- Messages: 585
- Enregistré le: 12 Déc 2011, 23:06
-
 par BiancoAngelo » 20 Déc 2014, 17:59
par BiancoAngelo » 20 Déc 2014, 17:59
Et c'est aussi que ce n'est pas la récurrence qu'on montre la deuxième, vu que :
si
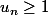
, alors

Et c'est fini.
-
BiancoAngelo
- Membre Rationnel
- Messages: 585
- Enregistré le: 12 Déc 2011, 23:06
-
 par BiancoAngelo » 20 Déc 2014, 18:01
par BiancoAngelo » 20 Déc 2014, 18:01
Il faudrait plutôt montrer correctement que
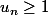
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 20 Déc 2014, 18:11
par adamNIDO » 20 Déc 2014, 18:11
BiancoAngelo a écrit:Il faudrait plutôt montrer correctement que
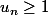
on peut pas dire : on voit facilement que
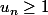
sinon on le montre comment
-
BiancoAngelo
- Membre Rationnel
- Messages: 585
- Enregistré le: 12 Déc 2011, 23:06
-
 par BiancoAngelo » 20 Déc 2014, 18:21
par BiancoAngelo » 20 Déc 2014, 18:21
adamNIDO a écrit:on peut pas dire : on voit facilement que
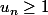
sinon on le montre comment
Si ça se voit facilement, on devrait pouvoir le montrer facilement...
Bon, les

étant par définition des racines carrées, on peut dire que
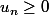
.
Or,
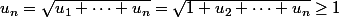
car
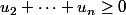
et
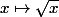
croissante.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 20 Déc 2014, 18:24
par zygomatique » 20 Déc 2014, 18:24
adamNIDO a écrit:on peut pas dire : on voit facilement que
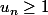
sinon on le montre comment
voir n'est pas une preuve !!!
il faut le démontrer !!!
d'autre part si u > 0 et
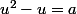
alors trivialement
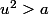
de façon tout aussi
minimaliste ...
donc la récurrence est triviale ....
(avec u >= 1 si nécessaire)
PS :: bien sur que c'est des inégalités larges ... détails typographique bien sur !!!
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 20 Déc 2014, 18:25
par adamNIDO » 20 Déc 2014, 18:25
BiancoAngelo a écrit:Si ça se voit facilement, on devrait pouvoir le montrer facilement...
Bon, les

étant par définition des racines carrées, on peut dire que
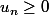
.
Or,
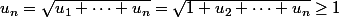
car
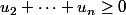
et
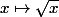
croissante.
merci infinement, mais
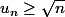
ne me permet pas de montrer que


-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 20 Déc 2014, 18:30
par zygomatique » 20 Déc 2014, 18:30
la relation
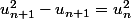
et la limite de u_n permettent de conclure en divisant par
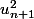
pour montrer que un >= 1
puisque u_n > 0
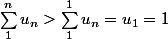
.... :ptdr:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 20 Déc 2014, 18:38
par adamNIDO » 20 Déc 2014, 18:38
zygomatique a écrit:la relation
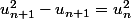
et la limite de u_n permettent de conclure en divisant par
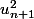
de vient cette relation est ce que lui aussi on doit la démontrer ou bien la remarque.
de plus si on a
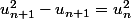
alors en divisant par
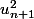
on obtient
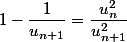
passant a la limite de

donne
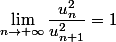
donc
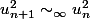
et par suite
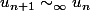
nest ce pas

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 20 Déc 2014, 18:50
par zygomatique » 20 Déc 2014, 18:50
adamNIDO a écrit:de vient cette relation est ce que lui aussi on doit la démontrer ou bien la remarque.
de plus si on a
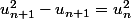
alors en divisant par
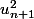
on obtient
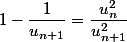
passant a la limite de

donne
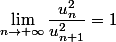
donc
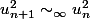
et par suite
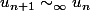
nest ce pas
oui et je l'espère pour la conclusion ... mais finalement je n'en suis plus aussi sur ....
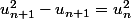
vient de la définition de la suite (u_n) ... voir post de BiancoAngelo ....
en notant u = u_n et v = u_{n + 1}
(v + u) = v (1 - u/v) = 1/(v + u))
serait peut-être plus juste ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités

sinon on le montre comment
alors en divisant par
on obtient

donc
et par suite