Salut, basons nous sur la propriété suivante que tu rappelles.
Maintenant, construisons une suite
)
de rationnels convergeante vers x et vérifiant :
pour tout n,

Déjà, on prend ce que l'on veut pour

qui soit strictement plus petit que

(aucune importance).
Soit n un entier différent de 0. Pour que tu comprennes bien, je reprends exactement tes notations. Si je note
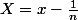
et
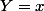
, alors
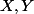
sont deux réels vérifiant
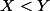
. On est donc sûr qu'il existe
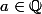
tel que
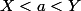
.
On choisit alors
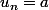
La suite
)
ainsi construite est une suite de rationnels et vérifie :
pour tout

Par le théorème des gendarmes, elle converge vers

et ainsi construite, c'est par valeurs inférieures.
Voilà, avec cet exemple, tu dois sûrement deviner comment construire la suite
)
.
Pseudo modifié : anciennement Trident2.
