Suite de rationnels

[Trident]

Bonsoir, je bloque sur un exercice dont j'ai une idée intuitive mais je ne vois pas trop comment la rédiger.

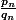
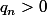
Soit (une suite de rationnels ; on écrit chaque sous forme de fraction irréductible, avec et on suppose que converge vers un élément .

1) On suppose que est bornée. Démontrer que est stationnaire.

2) On suppose que l est irrationnel. Démontrer que tend vers +oo.

Pour la 1) :
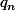
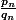
La suite est convergente donc en particulier de Cauchy donc les termes vont être de plus en plus proches les uns des autres. Je me doute bien que si on impose que ne dépasse pas un certain entier , alors les termes ne vont plus pouvoir suivre la cadence qui impose que les termes soient encore et toujours plus proches à chaque rang. Donc seule solution, les termes seront égaux pour répondre à l'exigence d'être une suite de Cauchy. C'est un peu mal dit mais voilà comment je ressent tout ça.

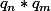
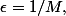
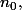
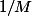
Si on regarde le max des combinaisons avec n, m dans N (qu'on note ) alors je pense qu'en posant c'est là que ça va coincer. A partir d'un rang les termes seront inférieurs à et ça va pas être possible mais je vois pas comment le prouver.


Pour la 2) :

Une nouvelle fois, intuitivement, je me doute que si la suite converge vers un irrationnel, alors les termes se rapprochent d'un irrationnel qui a un développement décimal infini donc ça va marcher. Car quelque soit la précision demandée,y'a de la matière pour se rapprocher de l étant donné qu'il a un développement décimal infini.


Merci bien.

[Doraki]

Pour la 1 c'est bien un truc comme ça qu'il faut faire.
On suppose (qn) bornée par M. Si t'appelles E(M) l'ensemble des fractions autorisées dans la suite (les fractions a/b avec 0 < b < M),
puisque la suite est de Cauchy il suffit de trouver un petit ;)(M)>0 tel que deux fractions distinctes quelconques de E(M) soient distantes d'au moins ;)(M). Puisque |a/b - c/d| = |ad-bc| / bd >= 1/bd > 1/M², on peut prendre ;)(M) = 1/M².

Pour le 2 pour montrer que ça tend vers l'infini ça revient à montrer que si l est irrationel alors pour tout M il existe un intervalle I(l,M) contenant l qui ne contient aucun élément de E(M). Ce qui est presque équivalent (puisque les irrationnels ne sont pas dans E(M)) à ce que le complémentaire de E(M) soit ouvert.

En fait si tu montres que le complémentaire de E(M) est ouvert (donc que E(M) est fermé), ça implique le résultat.

[Trident]

Pour la 1 c'est bien un truc comme ça qu'il faut faire.
On suppose (qn) bornée par M. Si t'appelles E(M) l'ensemble des fractions autorisées dans la suite (les fractions a/b avec 0 0 tel que deux fractions distinctes quelconques de E(M) soient distantes d'au moins (M). Puisque |a/b - c/d| = |ad-bc| / bd >= 1/bd > 1/M², on peut prendre (M) = 1/M².

Pour le 2 pour montrer que ça tend vers l'infini ça revient à montrer que si l est irrationel alors pour tout M il existe un intervalle I(l,M) contenant l qui ne contient aucun élément de E(M). Ce qui est presque équivalent (puisque les irrationnels ne sont pas dans E(M)) à ce que le complémentaire de E(M) soit ouvert.

En fait si tu montres que le complémentaire de E(M) est ouvert (donc que E(M) est fermé), ça implique le résultat.

Merci doraki, je vais lire ça.

Pour la 1), OK, c'était tout bête en fait.

Pour la 2), je ne vois pas pourquoi dire que q_n tend vers +oo revient à dire ce que tu dis.

[Ben314]

Salut,
Pour la 2), si "jeune mabuse", il suffit de démontrer la contraposée ce qui est assez évident à l'aide de la 1) :
Si on prend une suite convergente (vers L) de rationnnels pn/qn telle que la suite qn ne tende pas vers +oo alors on peut en extraire une sous suite telle que les qn restent bornés (et qui évidement continue à converger vers L).
Sauf que dans ce cas, le 1) implique que la suite est constante à partir d'un certain rang et donc que L est rationnel