Suite de rationnels
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
jonses
- Membre Relatif
- Messages: 496
- Enregistré le: 19 Mai 2013, 09:33
-
 par jonses » 12 Oct 2013, 19:26
par jonses » 12 Oct 2013, 19:26
Bonjour ou bonsoir,
Je suis bloqué sur une question qui me demande de montrer que "tout nombre réel est la limite d'une suite croissante de nombres rationnels".
J'ai procédé ainsi :
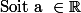
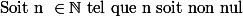
:
On a :
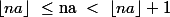
Donc :
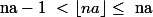
Je m'intéresse alors à la suite de terme général :
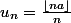
Cette suite est bien une suite de rationnels. Elle tend vers a quand n tend vers l'infini, mais je n'arrive pas à montrer qu'elle est croissante.
Est-ce que je dois utiliser une autre suite ? Si oui, alors je ne vois pas comment procéder
Je vous remercie d'avance pour vos réponses
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 12 Oct 2013, 20:41
par adrien69 » 12 Oct 2013, 20:41
Salut,
a-1)/na \geq 1 + (a-1)/(na))
C'est croissant
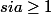
Sinon
a/(na-1)\leq 1 +(a-1)/(na-1))
Donc décroissant si
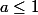
-
MMu
- Membre Relatif
- Messages: 399
- Enregistré le: 11 Déc 2011, 22:43
-
 par MMu » 12 Oct 2013, 20:43
par MMu » 12 Oct 2013, 20:43
Mais
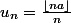
n'est ni croissante ni décroissante ! Tu n'as qu'à vérifier sur un exemple concret ..
Mais tu peux trouver une sous-suite croissante de

.
:zen:
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 12 Oct 2013, 20:56
par adrien69 » 12 Oct 2013, 20:56
J'ai dit de la merde. J'ai oublié un terme. Désolé.
-
jonses
- Membre Relatif
- Messages: 496
- Enregistré le: 19 Mai 2013, 09:33
-
 par jonses » 12 Oct 2013, 22:31
par jonses » 12 Oct 2013, 22:31
MMu a écrit:Mais
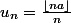
n'est ni croissante ni décroissante ! Tu n'as qu'à vérifier sur un exemple concret ..
Mais tu peux trouver une sous-suite croissante de

.
:zen:
Finalement, j'ai changé ma démarche (après pas mal de recherche sur des cours trouvés sur le net, donc c'est pas une démarche que j'ai pondue par miracle, disons que j'ai un peu triché, je sais c'est pas bien) :
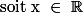

On a :
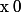
définie par :
le premier terme

et

Cette suite est bien croissante, à valeur dans les nombres rationnels, et a pour limite x
-
khalid92
- Membre Naturel
- Messages: 11
- Enregistré le: 09 Oct 2013, 14:00
-
 par khalid92 » 13 Oct 2013, 00:52
par khalid92 » 13 Oct 2013, 00:52
jonses a écrit:Finalement, j'ai changé ma démarche (après pas mal de recherche sur des cours trouvés sur le net, donc c'est pas une démarche que j'ai pondue par miracle, disons que j'ai un peu triché, je sais c'est pas bien) :
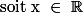

On a :
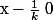
définie par :
le premier terme

et

Cette suite est bien croissante, à valeur dans les nombres rationnels, et à pour limite x (il suffit de montrer que pour entier naturel n :

, ce que j'ai fait par récurrence)
jaimerais savoir comment tu l'as fait par récurrence
-
jonses
- Membre Relatif
- Messages: 496
- Enregistré le: 19 Mai 2013, 09:33
-
 par jonses » 13 Oct 2013, 08:32
par jonses » 13 Oct 2013, 08:32
khalid92 a écrit:jaimerais savoir comment tu l'as fait par récurrence
Mince ça marche pas, je me suis trompé quelque part
Non!!! Je dois tout refaire !
Bon j'ai changé mes données dans le message précédent, donc j'ai refait ma récurrence. ça me donne ça, et normalement ça devrait aller (j'espère que je me suis pas encore trompé) :
Montrons par récurrence que :
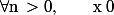
, supposons


vu que

et qu'entre

et
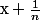
il existe un rationnel,
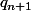
existe.
Donc on a bien

ça a l'air un peu bancal en fait
J'aurai encore besoin de votre aide svp
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 13 Oct 2013, 11:16
par Doraki » 13 Oct 2013, 11:16
Tu n'as toujours pas défini qn correctement.
(et puis on veut une suite croissante et non décroissante, non ?)
Disons que tu souhaites définir une suite croissante telle que x - 1/n < qn < x.
Ben tu fais :
- q1 doit vérifier x-1 < q1 < x. Donc on prend q1 un rationnel quelconque dans ]x-1 ; x[
- q2 doit vérifier x-1/2 < q2 < x et q1 < q2, donc on prend q2 un rationnel quelconque dans ]max(x-1/2 ; q1) ; x[
- q3 doit vérifier x-1/3 < q3 < x et q2 < q3, donc on prend q3 un rationnel quelconque dans ]max(x-1/3 ; q2) ; x[
etc.
Tu supposes (q1...q(n-1)) construits correctement, ben tu prends qn un rationnel quelconque dans ]max(x-1/n ; q(n-1) ; x[ (qui est un intervalle ouvert non vide parceque x-1/n < x et q(n-1) < x)
Par récurrence tu obtiens donc une suite infinie (qn) vérifiant ce qu'il faut, par construction.
-
jonses
- Membre Relatif
- Messages: 496
- Enregistré le: 19 Mai 2013, 09:33
-
 par jonses » 13 Oct 2013, 12:28
par jonses » 13 Oct 2013, 12:28
Merci,
Maintenant c'est vraiment plus clair !
Je manque vraiment de rigueur :mur:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
