Somme (ou produit...)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
flo22
- Membre Relatif
- Messages: 185
- Enregistré le: 08 Oct 2006, 18:01
-
 par flo22 » 15 Juil 2009, 16:55
par flo22 » 15 Juil 2009, 16:55
Bonjour à tous.
Je dois calculer une intégrale par une somme de Riemann, mais je bloque sur une somme...
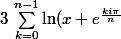)
ou bien ce produit
)
Merci !
HS : c'est la première fois que j'utilise latex, pourquoi les bornes ne sont pas au dessus du sigma et du pi ?
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 15 Juil 2009, 17:00
par Clembou » 15 Juil 2009, 17:00
flo22 a écrit:Bonjour à tous.
Je dois calculer une intégrale par une somme de Riemann, mais je bloque sur une somme...
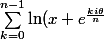)
ou bien ce produit
)
Merci !
HS : c'est la première fois que j'utilise latex, pourquoi les bornes ne sont pas au dessus du sigma et du pi ?
Note LaTeX : Utilises 3$ ou 4$ pour agrandir la formule. Tu verras les bornes seront au dessus et en dessous du symbole.
3$ \sum_{k=0}^{n-1} \ln(x+\mathrm{e}^\frac{k\mathrm{i}\theta}{n}) : )
-
Maks
- Membre Relatif
- Messages: 474
- Enregistré le: 14 Mai 2009, 21:03
-
 par Maks » 15 Juil 2009, 17:10
par Maks » 15 Juil 2009, 17:10
Sans changer la tailler, on peut simplement rajouter la balise \displaystyle au début du code.
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 15 Juil 2009, 17:12
par skilveg » 15 Juil 2009, 17:12
Tu es sûr que c'est pour un

quelconque et pas pour
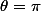
ou

?
-
flo22
- Membre Relatif
- Messages: 185
- Enregistré le: 08 Oct 2006, 18:01
-
 par flo22 » 15 Juil 2009, 17:16
par flo22 » 15 Juil 2009, 17:16
au temps pour moi :s C'est bien pour
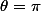

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 15 Juil 2009, 17:54
par Ericovitchi » 15 Juil 2009, 17:54
Déjà
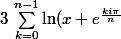 = ln ( \prod _{k=0}^{n-1} (x+e^{\frac{k i \pi}{n}}) ))
donc quand tu auras trouvé la première tu auras la seconde.
Sinon S(0) = (n-1) i pi mais bon ... ça ne sert pas à grand chose
Si S(x) =
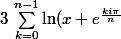)
On a envie de dériver car ça sera sûrement plus façile de trouver une réponse sous cette forme :
S'(x) =
})
Mais après je n'ai pas encore trouvé grand chose :hum:
C'est quoi l'intégrale ? je suis sûr que ça va nous inspirer.
-
flo22
- Membre Relatif
- Messages: 185
- Enregistré le: 08 Oct 2006, 18:01
-
 par flo22 » 15 Juil 2009, 18:06
par flo22 » 15 Juil 2009, 18:06
Oui c'est pour ça que j'ai l'une ou l'autre à trouver. Mais je pense que je dois aller sur une autre voix... Voici l'intégrale :
+x^2)d\theta)
Mais je pense que je vais devoir changer de stratégie.
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 15 Juil 2009, 18:10
par kazeriahm » 15 Juil 2009, 18:10
Non c'est bien comme méthode,
maintenant il faut regarder le produit des (x+exp(...)) et faire des regroupements de deux termes pour simplifier
-
ToToR_2000
- Membre Relatif
- Messages: 121
- Enregistré le: 26 Juin 2009, 17:33
-
 par ToToR_2000 » 15 Juil 2009, 18:15
par ToToR_2000 » 15 Juil 2009, 18:15
Bonjour,
l'idée de calculer une somme de Riemann pour trouver l'intégrale est bonne.
Pour calculer la somme des log, mets log(x) en facteur dans chacun des termes pour faire apparaître une somme de log(1+...) où le terme ... tend vers 0 quand n tend vers l'infini.
Ensuite, tu fais un petit dev limité et tu utilises un théorème de sommation d'équivalents (pour les séries): tu pourras en déduire un dév limité de la somme des log initiale quand n tend vers l'infini et avec ça tu devrais pouvoir conclure
(dis-moi si ça ne marche pas)
-
flo22
- Membre Relatif
- Messages: 185
- Enregistré le: 08 Oct 2006, 18:01
-
 par flo22 » 15 Juil 2009, 18:20
par flo22 » 15 Juil 2009, 18:20
J'ai remarqué que c'était un produit de la forme
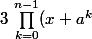)
mais bon...

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 15 Juil 2009, 18:21
par Ericovitchi » 15 Juil 2009, 18:21
Oui je serais toi je ferais f'(x) =
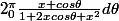
Et puis comme
(x+e^{-i\pi}))
ca devrait s'intégrer ça en décomposant en éléments simples ?
-
flo22
- Membre Relatif
- Messages: 185
- Enregistré le: 08 Oct 2006, 18:01
-
 par flo22 » 15 Juil 2009, 18:26
par flo22 » 15 Juil 2009, 18:26
L'énoncé précise qu'il faut le faire par Riemann.
Tutor je ne comprends pas trop : tu me dire de faire ceci :
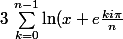=\sum \ln x + \sum \ln (1+\frac{e^{\frac{ki\pi}{n}}}{x}))
-
bobu
- Membre Naturel
- Messages: 64
- Enregistré le: 14 Juil 2009, 09:50
-
 par bobu » 15 Juil 2009, 19:03
par bobu » 15 Juil 2009, 19:03
Salut,
ca ne serait pas 2*i*k*pi/n au lieu de i*k*pi/n dans l'exponentiel?
car si c'est le cas j'ai trouvé comment le faire par Riemman...
-
flo22
- Membre Relatif
- Messages: 185
- Enregistré le: 08 Oct 2006, 18:01
-
 par flo22 » 15 Juil 2009, 19:18
par flo22 » 15 Juil 2009, 19:18
Je me serai trompé en faisant la somme de Riemann ? ça n'est pas :
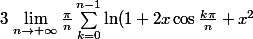)
-
bobu
- Membre Naturel
- Messages: 64
- Enregistré le: 14 Juil 2009, 09:50
-
 par bobu » 15 Juil 2009, 19:28
par bobu » 15 Juil 2009, 19:28
c'est bien une somme de riemman que tu as écrit, rassure toi! mais c'est juste qu'avec 2*pi et non pi j'arrive à une solution... qui vaut ce qu'elle vaut...
-
flo22
- Membre Relatif
- Messages: 185
- Enregistré le: 08 Oct 2006, 18:01
-
 par flo22 » 15 Juil 2009, 19:39
par flo22 » 15 Juil 2009, 19:39
Et c'est bien la bonne somme de Riemann, correspondant à l'intégrale recherchée ?
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 15 Juil 2009, 19:41
par Pythales » 15 Juil 2009, 19:41
Soit
=\int_0^{\pi}ln(1+2x\cos\theta+x^2)d\theta)
avec
=\int_0^{\pi}ln(1-2x\cos\theta+x^2)d\theta)
Le changement
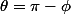
montre que
=I(x))
Donc
=lim_{n\rightarrow\infty}\frac{\pi}{n}ln\prod_0^{n-1}(1-2x\cos\frac{k\pi}{n}+x^2)=lim\frac{\pi}{n}ln[\frac{x-1}{x+1}(x^{2n}-1)])
à toi de conclure ...
-
bobu
- Membre Naturel
- Messages: 64
- Enregistré le: 14 Juil 2009, 09:50
-
 par bobu » 15 Juil 2009, 19:50
par bobu » 15 Juil 2009, 19:50
effectivement moi j'avais pris l'intégrale sur 0, 2*pi ... Désolé
-
flo22
- Membre Relatif
- Messages: 185
- Enregistré le: 08 Oct 2006, 18:01
-
 par flo22 » 15 Juil 2009, 20:07
par flo22 » 15 Juil 2009, 20:07
Je ne vois pas commence tu calcules le produit :s
-
bobu
- Membre Naturel
- Messages: 64
- Enregistré le: 14 Juil 2009, 09:50
-
 par bobu » 15 Juil 2009, 20:12
par bobu » 15 Juil 2009, 20:12
je pense qu'il à factorisé le x²-2xcos .... par (x-e(ikpi/n))(x-e(-ikpi/n)) et après il utilise le fait que les racines de X^(2n) - 1 sont les e(ik*pi/n)) ou un truc du genre...
Dites moi si je me trompe....
Rq : je n'utilise pas LATEX ca me gonfle...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 70 invités
)