Ce topic calcule:
On utilise les formules suivantes:
somme des (n+1) premiers termes d'une progression géométrique de raison z:
or:
De même:
d'où
Le quotient des sinus étant réel,
Somme de cosinus d'arcs en progression arithmétique
3 messages
- Page 1 sur 1
Somme de cosinus d'arcs en progression arithmétique
par mathelot » 10 Sep 2008, 05:07
Bjr,
Ce topic calcule:
+\cos(2 \alpha)+\cos(3 \alpha)+\cdots+\cos(n \alpha))
, 
étant un réel.
On utilise les formules suivantes:
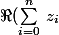=\sum_{i=0}^{n} \, \Re(z_i))
où _{i \in [0,n]})
sont (n+1) nombres complexes.
somme des (n+1) premiers termes d'une progression géométrique de raison z:
=\lambda \Re( z))
avec 
réel.
+\cos(2 \alpha)+\cos(3 \alpha)+\cdots+\cos(n \alpha)=\sum_{k=0}^{n} \, \Re( e^{ik\alpha}))
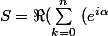}^{k}))
\alpha}}{1-e^{i\alpha}}))
or:
)
)
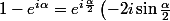De même:
\alpha}=e^{i \frac{(n+1)}{2}\alpha} \, \left(e^{ - i \frac{(n+1)}{2}\alpha} - e^{i \frac{(n+1)}{2}\alpha} \right))
\alpha}=e^{i \frac{(n+1)}{2}\alpha} \, \left( -2 i \sin \frac{(n+1)\alpha}{2} \right))
d'où
\alpha}{2} } {\sin \frac{\alpha}{2}} ))
Le quotient des sinus étant réel,
\alpha}{2} }{\sin \frac{\alpha}{2} } \, \Re( e^{i \frac{n\alpha}{2}}))
\alpha}{2}} {\sin \frac{\alpha}{2}} \, \cos \frac{n \alpha}{2})
Ce topic calcule:
On utilise les formules suivantes:
somme des (n+1) premiers termes d'une progression géométrique de raison z:
or:
De même:
d'où
Le quotient des sinus étant réel,
par fatal_error » 10 Sep 2008, 08:47
Ca aidera certainement ceux qui se taperont des réseaux d'antenne. Paix à leur TD :marteau:
la vie est une fête 
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 15 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :