Approximation d'une ellipse par des arcs de cercle

[niko003]

Salut,
mon objectif c'est de trouver l'angle téta, avec ce que tu proposes, j'arrive bien a calculer les coordonnées mais je pars du principe que je connais l'angle, hors je veux l'inverse : trouver pour quel angles j'ai mon quart d'ellipse découpé en 5 morceaux identiques.

[Ben314]

Par "morceaux identiques", tu veut dire de même longueur ou bien de même angle au centre ?
- Dans le premier cas, ça va forcément être un peu compliqué et passer par des calculs (ou des approximations) de la fameuse intégrale avec le ds de ton deuxième post.
- Dans le second cas, c'est évidement bien plus simple vu que la formule s'inverse on ne peut plus facilement en .

[niko003]

Malheureusement il s agit d avoir une longueur identique sur le périmètre de l ellipse donc le cas 1.
J ai déjà approximé l intégrale mentionnée dans le 2nd post (Simpson method sur 8 points)
Malheureusement elle ne colle pas tout à fait les résultats diverses de 0.1 à 1 degré

[Ben314]

J'ai pas mal l'impression que tu as pas le choix :
Tu as ta fonction donnant la longueur en fonction du paramétrage.
Tu doit calculer au plus précis la longueur du 1/4 d'ellipse .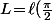
Puis déterminer les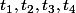 telles que en procédant soit par dichotomie, soit avec un truc style méthode des tangentes de Newton (vu que 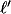est super simple) ce qui, de nouveau, demande à calculer des avec une certaine précision.

Après, je sais pas avec quoi tu compte faire les calculs, mais forcément qu'en approximant ton intégrale avec uniquement 8 points, ben ça va pas être bien précis comme résultat.