Progression arithmétique

par **GAW** » 28 Oct 2010, 17:12

Bonjour.

Avant les vacances j'ai eu une colle de maths et je dois en rendre un "compte-rendu" à la rentrée.

Voici l'énoncé:
"Trouver le nombre de progressions arithmétiques de 3 termes que l'on peut extraire des entiers 1, 2, ..., n."

Le colleur m'avait donné la réponse mais je dois dire que son écriture étais illisible et ma mémoire pas géniale..
Il y a de la partie entière, du carré et du divisé par 4. Dans le raisonnement il faut aussi séparer les cas n pair, n impair.

Voilà, si vous avez des idées je suis preneur !
Merci bien !

PS: Je ne suis pas là durant quelques jours (4), mais ne vous gênez pas pour ça !

par **Ben314** » 28 Oct 2010, 22:57

Salut,
Si j'ai tout bien compris, tu cherche les couples

tels que

,

et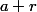

soient dans

.
Là ou la question n'est pas claire, c'est si l'on a le droit de prendre r=0 (c'est à dire considère t'on que l'on peut "extraire" trois fois le même nombre) ? et as-on le droit de prendre r<0, (considère t'on que "extraire" 1,2,3 est la même chose ou pas que "extraire" 3,2,1) ?

Si on considère

quelconque (i.e on peut extraire 5,5,5 et extraire 1,2,3 est différent de extraire 3,2,1) alors, pour

fixé, on doit prendre

tel que

et

,c'est à dire

et il y a donc

possibilités pour r.
Le nombre total de possibilités est donc :

par **GAW** » 02 Nov 2010, 12:45

Tout d'abord merci de ta réponse.

Mais non, les suites 1, 2, 3 et 3, 2, 1 sont les mêmes et la suite 5, 5, 5 n'existe pas... :mur:

par **Ben314** » 02 Nov 2010, 15:04

Dansx ce cas, il te suffit de reprendre la preuve ci dessus mais en rajoutant la condition r>0 : c'est exactement le même type de calculs.

par **GAW** » 02 Nov 2010, 15:43

Mais ici tu gardes que les suites 1, 2, 3 et 3, 2, 1 sont les mêmes...

En revanche: Comment arrives-tu à "il y a donc 2ma+1 possibilités pour r." ?

par **Ben314** » 02 Nov 2010, 16:03

GAW a écrit:Mais ici tu gardes que les suites 1, 2, 3 et 3, 2, 1 sont les mêmes...

Si tu impose r>0, ça signifie que 5,5,5 et 3,2,1 sont "interdites"

GAW a écrit:En revanche: Comment arrives-tu à "il y a donc 2ma+1 possibilités pour r." ?

Tu rigole ou quoi ?
L'ensemble {-3,-2,-1,0,1,2,3} contient combien d'éléments ? et {-m,-(m-1),...,-1,0,1,...,m-1,m} ?

par **GAW** » 02 Nov 2010, 18:45

Oui, c'est bon j'ai compris ! Excuse moi !!

Les vacances, c'est fatigant.. :dodo:

par **GAW** » 02 Nov 2010, 18:46

Merci bien !! Je suis déjà bien avancé, je verrai la suite.

Progression arithmétique

Progression arithmétique

Qui est en ligne