Séries entières, fonction exponentielle
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
yippeekiyay
- Messages: 6
- Enregistré le: 24 Aoû 2009, 12:46
-
 par yippeekiyay » 11 Juin 2013, 13:10
par yippeekiyay » 11 Juin 2013, 13:10
Bonjour,
[url]http://fr.wikiversity.org/wiki/Série_entière/Fonction_exponentielle[/url]
Comme le théorème est vrai pour tout z, lorsque z=0, exp(0)=1 ma question est la suivante:
La somme de 0 à l'infini de z^n/n! est donc aussi égale à 1, alors que je trouverais plus naturel que cette somme soit égale à 0 (car 0^n/n! = 0) ..
Il y a certainement quelque chose qui m'échappe si quelqu'un peut m'éclairer... Merci

-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 11 Juin 2013, 13:12
par Luc » 11 Juin 2013, 13:12
yippeekiyay a écrit:0^n/n! = 0
Bonjour,
cette égalité est vraie si

.
Donc tous les termes sont nuls pour

. Reste le terme pour n=0, qui vaut (0^0)/(0!)=1/1=1.
Après, quelle est ta définition de la fonction exponentielle? Car souvent on prend comme définition, justement, la somme de cette série entière (car on peut alors calculer l'exponentielle de pleins de trucs : réels, complexes, matrices,...)
-
yippeekiyay
- Messages: 6
- Enregistré le: 24 Aoû 2009, 12:46
-
 par yippeekiyay » 11 Juin 2013, 13:15
par yippeekiyay » 11 Juin 2013, 13:15
Luc a écrit:Bonjour,
cette égalité est vraie si

.
Donc tous les termes sont nuls pour

. Reste le terme pour n=0, qui vaut (0^0)/(0!)=1/1=1.
Et oui!! :marteau:
Merci!
-
yippeekiyay
- Messages: 6
- Enregistré le: 24 Aoû 2009, 12:46
-
 par yippeekiyay » 11 Juin 2013, 13:33
par yippeekiyay » 11 Juin 2013, 13:33
Alors finalement 0^0=1 cela me parait pas évident en écrivant la puissance avec l'exponentielle, c'est par convention c'est ça?
-
yippeekiyay
- Messages: 6
- Enregistré le: 24 Aoû 2009, 12:46
-
 par yippeekiyay » 11 Juin 2013, 13:42
par yippeekiyay » 11 Juin 2013, 13:42
(Ou même avec les régles sur les puissances x^P=x^0x^P donc si x différent de 0 on peut diviser par x^p donc x^0=1. Mais si x=0?)
-
mrif
- Membre Rationnel
- Messages: 527
- Enregistré le: 18 Mar 2013, 21:26
-
 par mrif » 11 Juin 2013, 14:29
par mrif » 11 Juin 2013, 14:29
yippeekiyay a écrit:Alors finalement 0^0=1 cela me parait pas évident en écrivant la puissance avec l'exponentielle, c'est par convention c'est ça?
Oui c'est une convention qui découle naturellement de la limite en 0 de la fonction
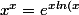})
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
