Bonjour,
Je ne sais répondre à rien à part les exos 2 et 4.
Pouvez-vous me donner des pistes ? Merci d'avance. Pas la solution entière svp, j'aime bien chercher.
https://www.docdroid.net/dLrBZv2/exercices-maths-2-pdf
Questions arithmétique
13 messages
- Page 1 sur 1
Re: Questions arithmétique
Je soupçonne le théorème de Wilson pour les exos 3 et 5. Et le petit théorème de Fermat pour l'exo 6.
Est-ce correct ? Par contre l'exo 1 je ne vois pas du tout quoi utiliser...
Est-ce correct ? Par contre l'exo 1 je ne vois pas du tout quoi utiliser...
Re: Questions arithmétique
Salut,
Je trouve que la façon dont les questions sont posées est on ne peut plus bizarre.
Exercice 3 :
Modulo de le traduire de façon plus compréhensible, l'énoncé demande de montre que, si est premier alors
est premier alors !-(p\!-\!2)) est congru à
est congru à  modulo
modulo  .
.
Et ça découle immédiatement du théorème de Wilson :!\equiv\!-1\ [p]) (facile à démontrer si tu ne l'a pas vu). Et l'hypothèse
(facile à démontrer si tu ne l'a pas vu). Et l'hypothèse  n'est pas utile.
n'est pas utile.
Par contre, je comprend absolument pas le sens de la prétendue indication : les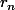 sont sensés être des "reste successifs". Je suppose que c'est des restes de divisions, mais de division de quoi par quoi ?
sont sensés être des "reste successifs". Je suppose que c'est des restes de divisions, mais de division de quoi par quoi ?
Je trouve que la façon dont les questions sont posées est on ne peut plus bizarre.
Exercice 3 :
Modulo de le traduire de façon plus compréhensible, l'énoncé demande de montre que, si
Et ça découle immédiatement du théorème de Wilson :
Par contre, je comprend absolument pas le sens de la prétendue indication : les
Modifié en dernier par Ben314 le 16 Déc 2023, 05:34, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Questions arithmétique
Salut,
Merci à toi, j'avais vu juste alors.
r est le reste de la division de (n-1)!-n par n+2
Merci à toi, j'avais vu juste alors.
r est le reste de la division de (n-1)!-n par n+2
Re: Questions arithmétique
Exercice 5 :
Montre que(b\!-\!1)+d\!-\!1}{2}\ \ \mbox{o\`u}\ \ d\!=\!\mbox{pgcd}(a,b)) .
.
Puis utilise simplement le fait que\ \Rightarrow\ a\!\equiv\!0\ [d]) qui suffit pour conclure.
qui suffit pour conclure.
Montre que
Puis utilise simplement le fait que
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Questions arithmétique
Merci beaucoup Ben314.
Pour l'exo 6 je peux utiliser le petit théorème de Fermat ?
Et pour l'exo 1 une idée svp ?
Merci.
Pour l'exo 6 je peux utiliser le petit théorème de Fermat ?
Et pour l'exo 1 une idée svp ?
Merci.
Re: Questions arithmétique
Exercice 6 :
C'est bien le petit théorème de Fermat qui fait marcher le bidule : le (encore une fois définie de façon saugrenue), c'est
(encore une fois définie de façon saugrenue), c'est  où
où  est le reste de la division de
est le reste de la division de  par
par 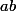 .
.
Le petit théorème de Fermat permet d'avoir facilement modulo
modulo  ainsi que
ainsi que  modulo
modulo  et avec ces deux infos, tu peut en déduire
et avec ces deux infos, tu peut en déduire  modulo
modulo 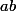 (sur le principe, c'est le théorème des restes chinois, mais ici, on peut facilement tout faire à la main) puis la valeur explicite de
(sur le principe, c'est le théorème des restes chinois, mais ici, on peut facilement tout faire à la main) puis la valeur explicite de  donc de
donc de  et on voit clairement que c'est un multiple de
et on voit clairement que c'est un multiple de  .
.
Je regarde le 1) (mais je fait autre chose en même temps . . .)
Tu as réussi à montrer l'indic que j'ai donné pour le 5 ?
(il faut évidement commencer par le cas où a et b sont premiers entre eux et il y a un petit truc à voir)
C'est bien le petit théorème de Fermat qui fait marcher le bidule : le
Le petit théorème de Fermat permet d'avoir facilement
Je regarde le 1) (mais je fait autre chose en même temps . . .)
Tu as réussi à montrer l'indic que j'ai donné pour le 5 ?
(il faut évidement commencer par le cas où a et b sont premiers entre eux et il y a un petit truc à voir)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Questions arithmétique
J'essaye, j'essaye...
Pour la 1 j'ai un début de démo.
Soit A=a^n-2
Grâce à la congruence, on a n divisant Phi(A)+2 en particulier comme 4 divise n on a 4 div Phi(A)+2 mais alors 4 ne divise pas Phi(A).
D'après ce post (https://math.stackexchange.com/question ... sible-by-4) alors forcément A=p^m ou A=2p^m m entier et p premier = 3 [4]
Par la formule de l'indicatrice qu'importe la forme de A On a alors Phi(A)= (p-1)*(p^(m-1)). Il faut montrer que m=1
Quelque soit la forme de A comme Phi a toujours la même valeur en injectant dans la congruence on a :
(p-1)p^m =-2 [n]
en particulier
(p-1)p^m = -2 [16]
2p^m = -2 [16]
p^m = -1 [8]
en particulier
p^m = -1 =3 [4]
Je crois que je me suis mélangé les pinceaux...
Pour la 1 j'ai un début de démo.
Soit A=a^n-2
Grâce à la congruence, on a n divisant Phi(A)+2 en particulier comme 4 divise n on a 4 div Phi(A)+2 mais alors 4 ne divise pas Phi(A).
D'après ce post (https://math.stackexchange.com/question ... sible-by-4) alors forcément A=p^m ou A=2p^m m entier et p premier = 3 [4]
Par la formule de l'indicatrice qu'importe la forme de A On a alors Phi(A)= (p-1)*(p^(m-1)). Il faut montrer que m=1
Quelque soit la forme de A comme Phi a toujours la même valeur en injectant dans la congruence on a :
(p-1)p^m =-2 [n]
en particulier
(p-1)p^m = -2 [16]
2p^m = -2 [16]
p^m = -1 [8]
en particulier
p^m = -1 =3 [4]
Je crois que je me suis mélangé les pinceaux...
Re: Questions arithmétique
J'ai pas le temps de chercher plus ce soir (autre chose à faire), mais j'avais plus ou moins fait les mêmes constats.
Attention (si tu veut rédiger propre) que pour avoir) pair, mais non divisible par 4, il y a aussi le cas particulier
pair, mais non divisible par 4, il y a aussi le cas particulier 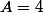 . Sauf qu'ici, c'est clairement impossible.
. Sauf qu'ici, c'est clairement impossible.
Et sinon, ce résultat est assez trivial vu que, si alors
alors \!=\!\prod (p_i\!-\!1)p_i^{\lambda_i-1}) où les
où les  sont pairs sauf pour
sont pairs sauf pour  . Donc s'il y en a deux ou plus, le résultat est multiple de 4.
. Donc s'il y en a deux ou plus, le résultat est multiple de 4.
Sinon, un autre truc que j'ai essayé (sans succès pour le moment), c'est d'utiliser le fait que, si\!=\!1) alors
alors }\!\equiv\!1\ [m]) . Avec
. Avec  et
et 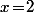 ou
ou  (en supposant
(en supposant  impair), on arrive à écrire des trucs, mais rien de concluant pour le moment.
impair), on arrive à écrire des trucs, mais rien de concluant pour le moment.
Attention (si tu veut rédiger propre) que pour avoir
Et sinon, ce résultat est assez trivial vu que, si
Sinon, un autre truc que j'ai essayé (sans succès pour le moment), c'est d'utiliser le fait que, si
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Questions arithmétique
J'ai l'impression de tomber sur un truc bizarre, à savoir qu'il n'y a pas de solutions pour l'exercice 1 (donc c'est pas faux de dire que dans ce cas le bidule est premier vu qu'il n'y a pas de tel cas . . .)
Vu que\!\equiv\!-2\ [16]) donc il est pair et non multiple de 4 ce qui implique que
donc il est pair et non multiple de 4 ce qui implique que  est soit égal à 4 (exclu vu que
est soit égal à 4 (exclu vu que  ), soit à
), soit à  , soit à
, soit à  avec, dans les deux cas
avec, dans les deux cas  premier et
premier et  pour que le
pour que le 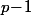 de
de ) soit divisible par 2, mais pas par 4.
soit divisible par 2, mais pas par 4.
On a forcément car :
car :
 }\Rightarrow\ p^{\lambda}\!\equiv\!-1\ [8])
 }\Rightarrow\ p^{\lambda}\!\equiv\!-1\ [8])
Mais\!=\!(p\!-\!1)p^{\lambda}\!\equiv\!-2\ [16]) c'est à dire
c'est à dire  donc
donc  et
et  .
.
Sauf qu'un nombre congru à 3 mod. 16 (donc mod. 8), à la puissance , ça ne donne jamais -1 mod. 8.
, ça ne donne jamais -1 mod. 8.
Vu que
On a forcément
Mais
Sauf qu'un nombre congru à 3 mod. 16 (donc mod. 8), à la puissance
Modifié en dernier par Ben314 le 16 Déc 2023, 20:34, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Questions arithmétique
J'ai une piste.
La conjecture 3.2 de ce papier : https://arxiv.org/pdf/2001.09617.pdf impliquerait la conjecture du problème 1.
La conjecture 3.2 de ce papier : https://arxiv.org/pdf/2001.09617.pdf impliquerait la conjecture du problème 1.
Re: Questions arithmétique
Tu as trouvé une erreur dans mon message précédent ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Questions arithmétique
Là comme ça non mais que penses-tu de mon message précédent ? À savoir que la conjecture du papier cité sur arxiv impliquerait ma conjecture ?
Je n'en suis pas certain.
Je n'en suis pas certain.
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
