3 Questions sur l'arithmétique!
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 24 Jan 2008, 14:07
par raito123 » 24 Jan 2008, 14:07
Bonjours,
Je revise cette leçon que j'aurai dû faire l'année derniére et je bloque sur trois exercice :
1*Déterminer l'ensemble :
)
2*Résoudre dans

:
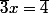
3*Résoudre dans

:
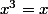
.
Je voudrais savoir comment ça se passe!!!!!
Merci
Les multiples ne doivent pas être utilisés sans nécessité
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 24 Jan 2008, 14:55
par tize » 24 Jan 2008, 14:55
Salut,
c'est assez simple,

veut dire qu'il existe un entier k tel que
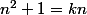
mais alors
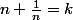
serait un entier ce qui n'est possible que si ....
2) et 3) les groupes ne contiennent que peu d'éléments on peut tester toute les valeurs de x...
-
MathMoiCa
- Membre Rationnel
- Messages: 518
- Enregistré le: 20 Jan 2008, 12:57
-
 par MathMoiCa » 24 Jan 2008, 15:08
par MathMoiCa » 24 Jan 2008, 15:08
Hello,
Pour le premier, on peut procéder ainsi : n²+1 multiple de n. Or, n² multiple de n, donc 1 multiple de n.
Pour le deuxième, il suffit de trouver l'inverse de la classe de 3 dans Z/8Z, ce qui est possible puisque 3 et 8 sont premiers entre eux.
Et pour le troisième plussun tize :id:
M.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 24 Jan 2008, 16:35
par ThSQ » 24 Jan 2008, 16:35
Oui mais quand même

est un corps (intègre donc) et
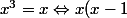(x+1) = 0)
...

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 24 Jan 2008, 18:00
par raito123 » 24 Jan 2008, 18:00
Dans le premier il y avait une faute dans l'énoncé c'est pas [n] mais [n+1] l'essentiel c'est que j'ai compris comment ça marche merci!!!
pour 2) et 3) je cherche et je reviens!!!
Les multiples ne doivent pas être utilisés sans nécessité

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 24 Jan 2008, 19:16
par leon1789 » 24 Jan 2008, 19:16
Bonjour
raito123 a écrit:Déterminer l'ensemble :
)
-1- Analyse :
Partons du fait que
)
divise
)
.
Posons d=n+1, on a alors n=-1 [d], donc n^2 = 1 [d]. Or d divise
)
, donc
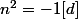
. Ainsi on a
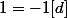
, donc 2=0[d], donc d divise 2, donc

, donc

-2- Synthèse :
Vérifier si -3, -2, 0, 1 sont solutions...

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 24 Jan 2008, 21:10
par raito123 » 24 Jan 2008, 21:10
Ok!merci.
Pour 2) et 3) j'ai trouvé
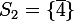
et
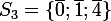
Quelqu'un peut-il confirmer?
Merci
Les multiples ne doivent pas être utilisés sans nécessité
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 24 Jan 2008, 21:30
par tize » 24 Jan 2008, 21:30
Je confirme :we:

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 24 Jan 2008, 21:32
par raito123 » 24 Jan 2008, 21:32
tize a écrit:Je confirme :we:
Merci je pars du bon pied!!!!:lol4:
Les multiples ne doivent pas être utilisés sans nécessité
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités