Questions d'arithmétique
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
savan-306D
- Membre Naturel
- Messages: 64
- Enregistré le: 24 Nov 2013, 23:39
-
 par savan-306D » 31 Mar 2014, 13:23
par savan-306D » 31 Mar 2014, 13:23
Salut, j'ai besoin d'aide dans deux problèmes d'arithmétique
le premier :
Démontrez

est un carré parfait.
le deuxième :
!}{k}})
est divisible par

Pour le deuxième, j'ai procédé par récurrence mais je n'ai arrivé à rien,
Le premier c'est un peu dur, bon voila ce qui m'a tombé par la tête:
on a kxy=x^2 + y^2 -x donc (x+y)^2 = x(1 + (k-2)y) mais je ne sais pas si cela pose une condition sur x ou non.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 31 Mar 2014, 14:18
par Ben314 » 31 Mar 2014, 14:18
Salut,
Il y a sans doute des tes de solutions plus ou moins directe...
Soit
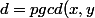)
.
Comme

on a

or

et

donc en fait

.
On peut donc écrire

,
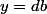
avec évidement
=1^{})
.
On a donc

c'est à dire

ce qui implique que

et donc que

vu que
=1^{})
.
Conclusion :

Pour le deuxième, c'est (2n)! ou bien 2(n!) le numérateur ?
Vu comme tu l'écrit, c'est 2(n!) sauf que dans ce cas, le 2 ne sert absolument à rien...
De plus, ta somme, ça m'étonnerais fort qu'elle commence à k=0...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
savan-306D
- Membre Naturel
- Messages: 64
- Enregistré le: 24 Nov 2013, 23:39
-
 par savan-306D » 31 Mar 2014, 21:57
par savan-306D » 31 Mar 2014, 21:57
Non ça ne commence pas à zero je viens de la modifier

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 01 Avr 2014, 06:48
par Ben314 » 01 Avr 2014, 06:48
Pour n=1
!}{k}}=2)
n'est pas divisible par

...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
savan-306D
- Membre Naturel
- Messages: 64
- Enregistré le: 24 Nov 2013, 23:39
-
 par savan-306D » 01 Avr 2014, 13:15
par savan-306D » 01 Avr 2014, 13:15
oui j'ai du faire une erreur en copiant le problème ce n'est pas juste pour 2 aussi

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 01 Avr 2014, 14:02
par Ben314 » 01 Avr 2014, 14:02
Un énoncé qui semble correct, c'est :
Montrer que, pour tout
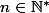
,
!}{k}})
est divisible par

.
Mais c'est trés "couillon" vu que
!}{k}}+{\frac{(2n)!}{2n+1-k}}\Big)=(2n+1)\sum_{k=1}^{n}{\frac{(2n)!}{k(2n+1-k)}})
où
!}{k(2n+1-k)}}\)
est entier vu que

et

sont deux termes
différents du produit qu'est
!)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
savan-306D
- Membre Naturel
- Messages: 64
- Enregistré le: 24 Nov 2013, 23:39
-
 par savan-306D » 01 Avr 2014, 22:09
par savan-306D » 01 Avr 2014, 22:09
T'as raison concernant l'énoncé c'est plutôt 2n, désolé pour ça.
J'ai réussi le premier exercice, même truc j'ai démontré

mais en montrant que
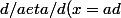)
-
savan-306D
- Membre Naturel
- Messages: 64
- Enregistré le: 24 Nov 2013, 23:39
-
 par savan-306D » 05 Avr 2014, 10:15
par savan-306D » 05 Avr 2014, 10:15
Il y a une autre solution : en utilisant une lemme si 2n+1 n'est pas premier
2n+1 divise
!}{k})
Donc si 2n+1 n'est pas premier, il divise
!}{k}})
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 20 invités
