Concernant ce que dit pascal, ça n'a pas trop de lien avec la théorie de la mesure : quand on parle de mesure sur R sans précision, ça signifie qu'on prend la mesure de Lebesgue et la tribu des Boréliens (voire la tribu complétée).
Or, par définition, la tribu des Boréliens contient tout les ouvert et tout les fermés de R ainsi que leur réunion/intersection au plus dénombrable donc évidement, ça contient tout les intervalles (ouvert, fermé ou semi-ouvert) donc ça contient bien tout les [1/n,1] ainsi que ]0,1].
Et dans ce cas de figure, la dénombrable additivité de la mesure de Lebesgue, ça te dit que la mesure des intervalles [1/n,1], (à savoir 1-1/n) tend vers la mesure de ]0,1], (à savoir 1).
Sinon, ça :
croco4 a écrit:
Alors par définition de
 = \beta(A_{n})~\forall n \in \mathbb{N})
On a:
 = \lim \alpha( A_{n}))
par additivité
(1) de la mesure

,
Et
 = \lim \beta( A_{n}))
par définition de
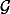 (2)
(2)de plus,
 = \lim \beta( A_{n}) < \infty) (3)
(3) car par hypothèse

sont finies.
Ainsi:

entraine

.
Conlusion
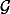
est bien une classe monotone.
c'est parfaitement O.K. modulo quelques mini détails sans grande importance :
(1) La plupart des auteurs préfèrent écrire complètement "par additivité
dénombrable" ou bien "par

-additivité" (qui veut dire exactement la même chose mais... c'est plus court à écrire...)
(2) A mon avis, là, ton "par définition de
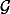
", il embrouille plus qu'autre chose : tu as déjà écrit que, par définition de
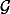
, on a
 = \beta(A_{n}))
et a mon sens, si tu veut mettre un "car quelque_chose" à cet endroit, il vaudrait mieux écrire "car
 = \beta(A_{n}))
"
(3) Le fait que les deux limites soient finies, c'est pas faux, mais je suis pas bien sûr que ça serve à quoi que ce soit dans le raisonnement. A ton sens, ça apporte quoi de dire que les limites sont finies ?

